12 Varianciák elemzése

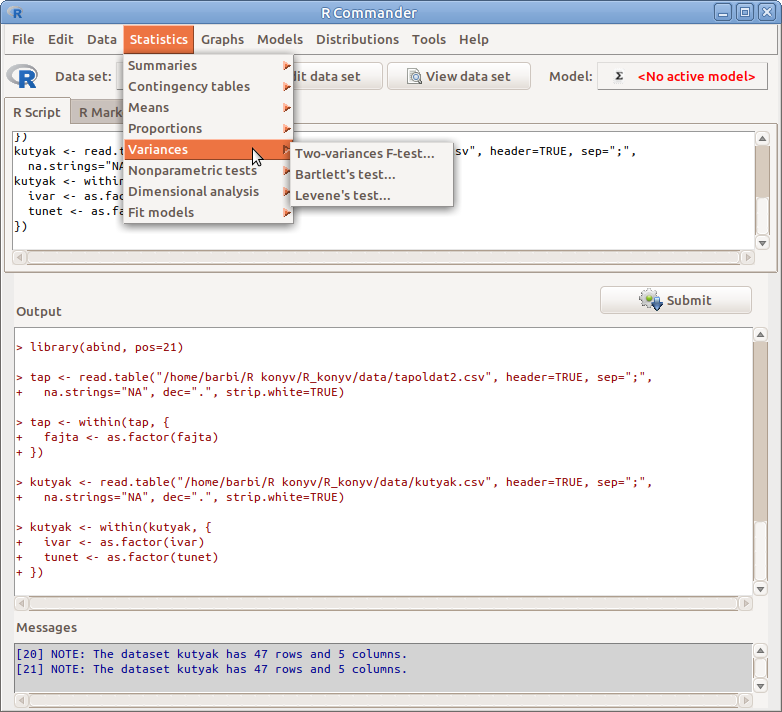
ábra Varianciák elemzése: *Statistics → Variances*

12.1: ábra Varianciák elemzése: Statistics → Variances

Varianciák elemzésére szolgáló eljárásokat a Statistics → Variances menüben találunk (12.1. ábra).

A Bartlett-próba (Bartlett’s test) az \(F\)-próba többmintás változata, a Levene-próbához hasonlóan kell paraméterezni (a középérték (Center) beállításától eltekintve).

12.1 Két, független mintás F-próba

Példánkban az vizsgáljuk kétmintás F-próbával (Statistics → Variances → Two variances F-test…), hogy egy keltetőgép felülvizsgálatakor ugyanolyan jó-e, ha alacsonyabb (\(36^\circ\)C), illetve ha magasabb (\(44^\circ\)C) hőfokot állítanak be rajta. (12.2. ábra, kelteto.csv). Ehhez meg kell adnunk a következőket:

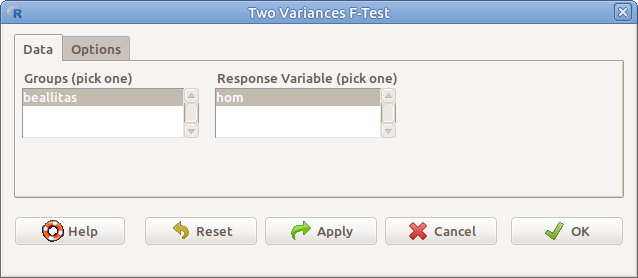
ábra *F*-próba: *Statistics → Variances → Two variances F-test...*

12.2: ábra F-próba: Statistics → Variances → Two variances F-test…

  • Groups (pick one) Csoportosító változó (2 szintű faktor lehet)
  • Response variable (pick one) A vizsgálandó változó

Az Options Az megjelenő párbeszéd ablakban pedig a következőket:

  • Ratio A hányados
  • Alternative Hypothesis - Two-sided \(H_1: \sigma^2_1 \neq \sigma^2_2\) - Ratio < 1 \(H_1: \sigma^2_1 < \sigma^2_2\) - Ratio > 1 \(H_1: \sigma^2_1 > \sigma^2_2\)
  • Confidence Level A mintákból becsült populációs varianciák hányadosára vonatkozó konfidencia-intervallum megbízhatósági szintje.
ábra *F*-próba beállítások: *Statistics &rarr; Means &rarr; Independent samples t-test...&rarr; Options*

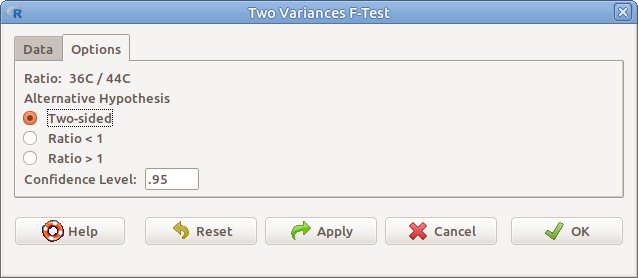
12.3: ábra F-próba beállítások: Statistics → Means → Independent samples t-test…→ Options

A teszt outputjában megkapjuk a \(F\)-statisztika értékét, a számláló (num df) és a nevező szabadsági fokát (denom df) és a \(p\)-értéket (p-value). Ezen kívül, kapunk egy – az alternatív hipotézis típusának megfelelő – konfidencia intervallumot a populációs varianciák hányadosára, valamint a mintából számolt varianciák hányadosát.

var.test(hom ~ beallitas, alternative='two.sided', 
     conf.level=.95, data=kelteto)
## 
##  F test to compare two variances
## 
## data:  hom by beallitas
## F = 0.24117, num df = 9, denom df = 9, p-value = 0.04565
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.05990248 0.97093703
## sample estimates:
## ratio of variances 
##           0.241167

(TK. 7.2.2. fejezet, 7.4. példa)

12.2 Levene-próba

Az előző fejezetben szereplő példánkat elemezzük Levene-próbával (Statistics → Variances → Levene’s test…, 12.4. ábra, kelteto.csv). Ehhez meg kell adnunk a következőket:

  • Factors (pick one) Csoportosító változó
  • Response variable (pick one) A vizsgálandó változó
  • Center Középérték típusa
    • Median Medián, inkább ezt használjuk!
    • Mean Átlag, eredeti Levene-próba
ábra Levene-próba: *Statistics &rarr; Variances &rarr; Levene's test...*

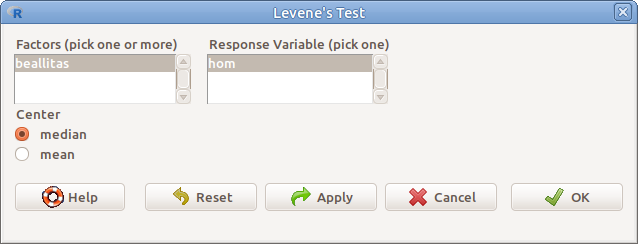
12.4: ábra Levene-próba: Statistics → Variances → Levene’s test…

A teszt outputjában megkapjuk a szabadsági fokokat (df), az \(F\)-statisztika értékét és a \(p\)-értéket (Pr(>F)).

leveneTest(kelteto$hom, kelteto$beallitas, center="median", data = kelteto)
## Levene's Test for Homogeneity of Variance (center = "median": kelteto)
##       Df F value  Pr(>F)  
## group  1  8.0907 0.01076 *
##       18                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(TK. 7.2.2. fejezet)