17 Eloszlások

Ezzel a menüvel (Distributions) lehet folytonos (Continuous distributions) illetve diszkrét eloszlásokból (Discret distributions) valószínűségeket és kvantiliseket (\(p\)-kvantilis: a valószínűségi változó azon értéke, amelynél kisebb értékek hányada \(p\)) számoltatni, illetve kirajzoltatni a megfelelő eloszlást, sűrűségfüggvényt, eloszlásfüggvényt, illetve adott eloszlású véletlen számokat generálni. A véletlen szám generáláshoz be lehet állítani a magot, ami a véletlen számok reprodukálhatóságát biztosítja (Set random number generator seed). Az egyes eloszlások esetén nagyon hasonló a működése, ezért csak egy-egy példát mutatunk folytonos (normális), illetve diszkrét (binomiális) eloszlásra.

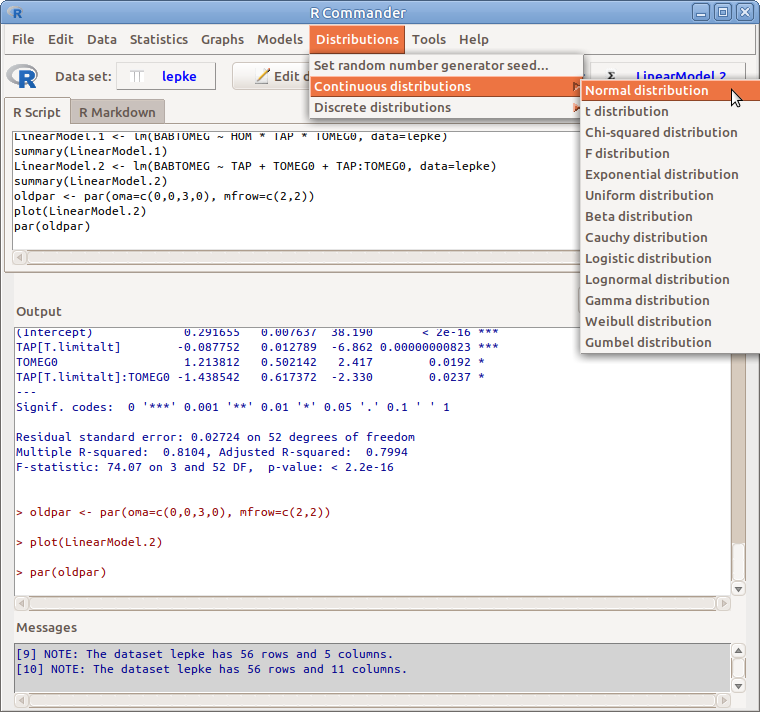
ábra Normális eloszlás menü: *Distributions → Continuous distributions → Normal distribution*

17.1: ábra Normális eloszlás menü: Distributions → Continuous distributions → Normal distribution

17.1 Folytonos eloszlás: normális

  • Normal quantiles… Normális eloszlás kvantilisei
  • Normal probabilities… Valószínűségek normális eloszlásból
  • Plot normal distribution… Normális eloszlás ábrázolása
  • Sample from normal distribution… Mintavétel normális eloszlásból

17.1.1 Adott valószínűséghez tartozó kvantilisek meghatározása

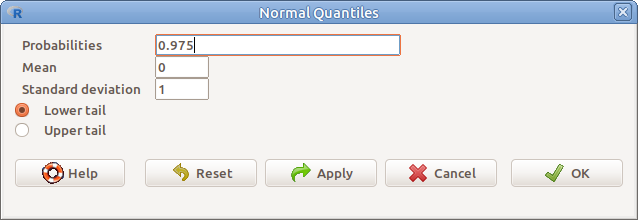
ábra Normális eloszlás kvantilisének meghatározása: *Distributions → Continuous distributions → Normal distribution → Normal quantiles*

17.2: ábra Normális eloszlás kvantilisének meghatározása: Distributions → Continuous distributions → Normal distribution → Normal quantiles

A kvantilisek meghatározásához a következőket kell megadni:

  • Probabilities Valószínűségek (vesszővel elválasztva)
  • Mean A normális eloszlás átlaga
  • Standard deviation A normális eloszlás szórása
  • Lower tail Az eloszlás alsó széle
  • Upper tail Az eloszlás felső széle
qnorm(c(0.975), mean=0, sd=1, lower.tail=TRUE)
## [1] 1.959964

17.1.2 Adott kvantilisekhez tartozó valószínűségek meghatározása

A valószínűségek meghatározásához a következőket kell megadni:

  • Variable value(s) A változó értékei (kvantilisek), vesszővel elválasztva
  • Mean A normális eloszlás átlaga
  • Standard deviation A normális eloszlás szórása
  • Lower tail Az eloszlás alsó széle
  • Upper tail Az eloszlás felső széle
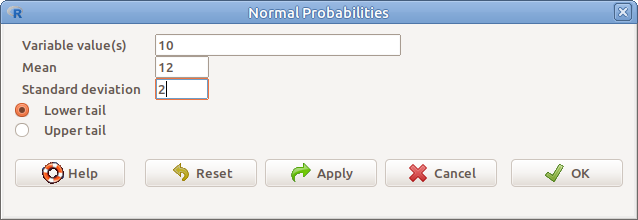
ábra Valószínűség meghatározása adott kvantilishez: Distributions → Continuous distributions → Normal distribution → Normal probabilites

17.3: ábra Valószínűség meghatározása adott kvantilishez: Distributions → Continuous distributions → Normal distribution → Normal probabilites 

pnorm(c(10), mean=12, sd=2, lower.tail=TRUE)
## [1] 0.1586553

17.1.3 Sűrűség-, illetve eloszlásfüggvény ábrázolása

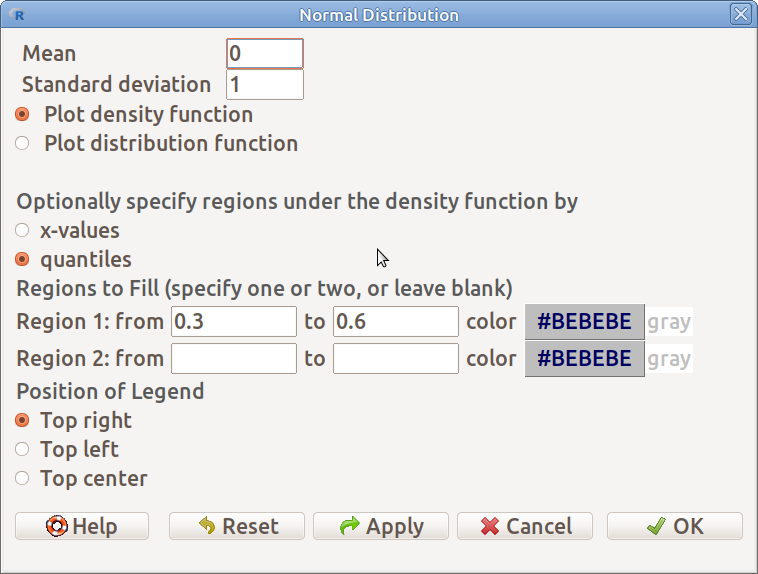
ábra *Sűrűség-, illetve eloszlásfüggvény ábrázolása: Distributions → Continuous distributions → Normal distribution → Plot normal distribution*

17.4: ábra Sűrűség-, illetve eloszlásfüggvény ábrázolása: Distributions → Continuous distributions → Normal distribution → Plot normal distribution

A függvények ábrázolásához a következőket kell megadni:

  • Mean A normális eloszlás átlaga
  • Standard deviation A normális eloszlás szórása
  • Plot density function Sűrűségfüggvény vagy
  • Plot distribution function Eloszlásfüggvény

Sűrűségfüggvény választása esetén lehetőség van arra is, hogy görbe alatti területeket ábrázoljunk a változó adott értéktartományában. Az értéktartomány megadható a “tól”, “ig” értékekkel , illetve adott valószínűségek megadásával. Ekkor a hozzájuk tartozó kvantilisek közötti területet fogja besatírozni a program.

  • Optionally specify regions under the density function by
    • x-values A változó értékeit adjuk meg
    • quantiles Valószínűségeket adunk meg, és az ezekhez tartozó kvantilisek közti területet színezi.
  • Regions to Fill (specify one or two, or leave blank) Nulla, egy vagy két tartomány megadása
    • Region 1:from to color tól-ig, szín megadása
    • Region 2:from to color tól-ig, szín megadása
  • Position of Legend Címke pozíciója
    • Top right Jobb fent
    • Top left Bal fent
    • Top center Középen fent

A @ref(fig.normsur). ábra a 17.4. ábrán bemutatott beállításokkal készült úgy, hogy a görbe alatti területet a 0.3 és 0.6 kvantilisek között mutatja.

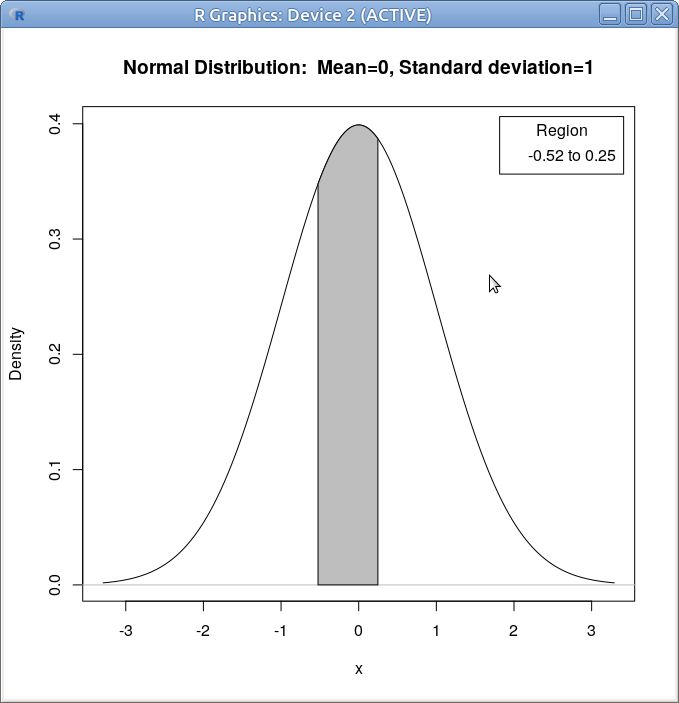
ábra Normális eloszlás sűrűségfüggvénye

17.5: ábra Normális eloszlás sűrűségfüggvénye

17.1.4 Mintavétel

Ezzel a lehetőséggel véletlen normális eloszlású mintákat készíthetünk (Distributions → Continuous distributions → Normal distribution → Sample from normal distribution). A mintaelemeket a mintaátlagokkal, szórásokkal, és a mintaelemek összegével együtt (ha bejelöljük) egy adattáblázatba írja bele a program, melyet menthetünk.

Megadandó:

  • Enter name of data set: Adattáblázat neve
  • Mean A normális eloszlás átlaga
  • Standard deviation A normális eloszlás szórása
  • Number of samples (rows) Minták (sorok) száma
  • Number of observations (columns) Mintaelemek (oszlopok) száma mintánként
  • Add to Data Set Adattáblázatba kiírandó
    • Sample means Mintaátlagok
    • Sample sums Mintaelemek összege
    • Sample standard deviations Minta szórások
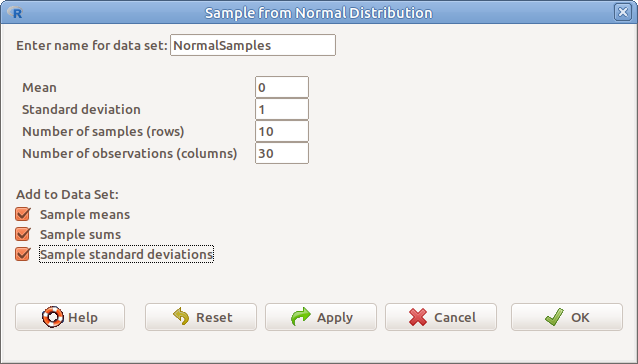
ábra *Mintavétel normális eloszlásból: Distributions → Continuous distributions → Normal distribution → Sample from normal distribution*

17.6: ábra Mintavétel normális eloszlásból: Distributions → Continuous distributions → Normal distribution → Sample from normal distribution

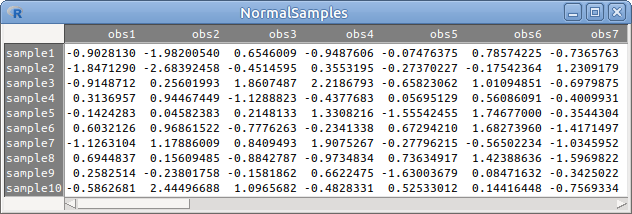
ábra Minták normális eloszlásból

17.7: ábra Minták normális eloszlásból

(TK. 3.5.4. fejezet 3.10. példa)

17.2 Diszkrét eloszlás: binomiális

A diszkrét eloszlások közül a – talán leggyakrabban használt – binomiális eloszlással kapcsolatos műveleteket mutatjuk be (17.8. ábra).

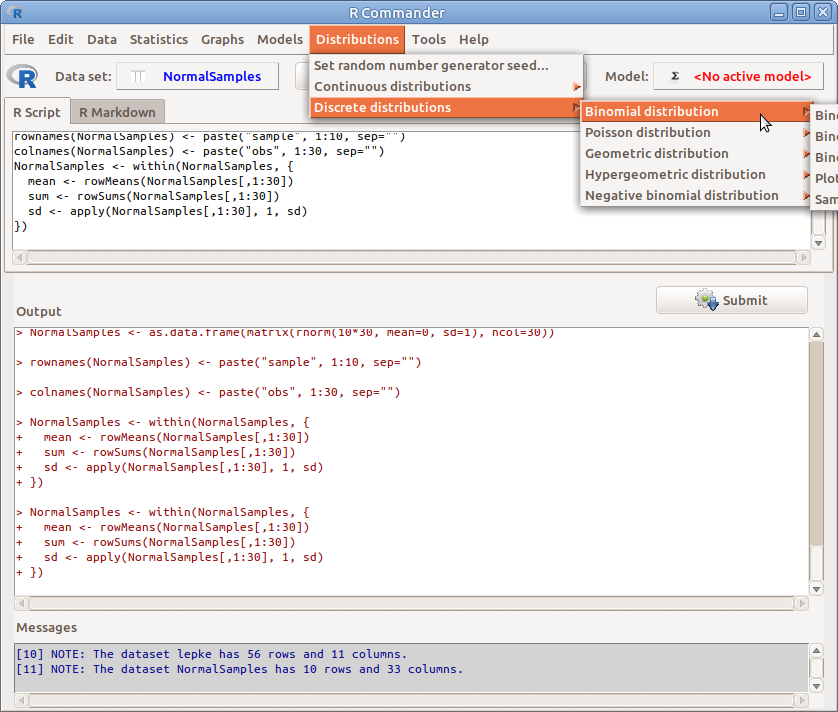
ábra Binomális eloszlás menü: *Distributions → Discrete distributions → Binomial distribution*

17.8: ábra Binomális eloszlás menü: Distributions → Discrete distributions → Binomial distribution

  • Binomial quantiles… Binomiális eloszlás kvantilisei
  • Binomial tail probabilities… Széli valószínűségek binomiális eloszlásból
  • Binomial probabilities… Valószínűségek binomiális eloszlásból
  • Plot binomial distribution… Binomiális eloszlás ábrázolása
  • Sample from binomial distribution… Mintavétel binomiális eloszlásból

17.2.1 Adott valószínűségekhez tartozó kvantilisek meghatározása

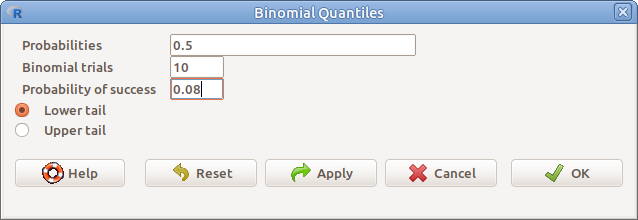
ábra Binomiális eloszlás kvantilise: Distributions → Discrete distributions → Binomial distribution* → Binomial quantiles*

17.9: ábra Binomiális eloszlás kvantilise: Distributions → Discrete distributions → Binomial distribution* → Binomial quantiles*

A kvantilis meghatározásához a következőket kell megadni:

  • Probabilities Valószínűségek (vesszővel elválasztva)
  • Binomial trials Kísérletek száma
  • Probability of success A bekövetkezés valószínűsége
  • Lower tail Az eloszlás alsó széle
  • Upper tail Az eloszlás felső széle
qbinom(c(0.5), size=10, prob=0.08, lower.tail=TRUE)
## [1] 1

17.2.2 Adott kvantilisekhez tartozó széli valószínűségek meghatározása

A valószínűségek meghatározásához a következőket kell megadni:

  • Variable value(s) A változó értékei (kvantilisek), vesszővel elválasztva
  • Binomial trials Kísérletek száma
  • Probability of success A bekövetkezés valószínűsége
  • Lower tail Az eloszlás alsó széle
  • Upper tail Az eloszlás felső széle
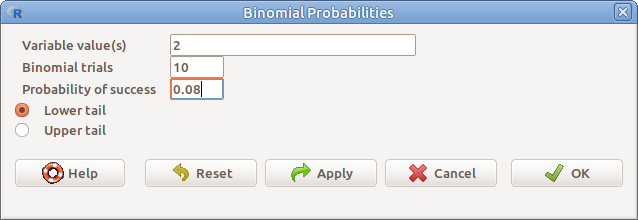
ábra Széli valószínűség meghatározása adott kvantilishez: *Distributions → Discrete distributions → Binomial distribution → Binomial tail probabilites*

17.10: ábra Széli valószínűség meghatározása adott kvantilishez: Distributions → Discrete distributions → Binomial distribution → Binomial tail probabilites 

pbinom(c(2), size=10, prob=0.08, lower.tail=TRUE)
## [1] 0.9599246

17.2.3 Adott kvantilisekhez tartozó valószínűségek meghatározása

A valószínűség meghatározásához a következőket kell megadni:

  • Binomial trials Kísérletek száma
  • Probability of success A bekövetkezés valószínűsége
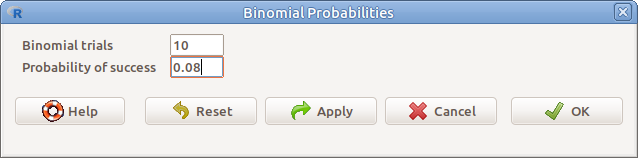
ábra Valószínűségek meghatározása adott kvantilisekhez: *Distributions → Discrete distributions → Binomial distribution → Binomial probabilites*

17.11: ábra Valószínűségek meghatározása adott kvantilisekhez: Distributions → Discrete distributions → Binomial distribution → Binomial probabilites 

.Table <- data.frame(Pr=dbinom(0:10, size=10, prob=0.08))
rownames(.Table) <- 0:10
.Table
##              Pr
## 0  4.343885e-01
## 1  3.777291e-01
## 2  1.478070e-01
## 3  3.427410e-02
## 4  5.215623e-03
## 5  5.442389e-04
## 6  3.943760e-05
## 7  1.959633e-06
## 8  6.390106e-08
## 9  1.234803e-09
## 10 1.073742e-11

17.2.4 Eloszlás ábrázolása

ábra Binomiális eloszlás ábrázolása: *Distributions &rarr; Disctrete distributions &rarr; Binomial distribution &rarr; Plot binomial distribution*

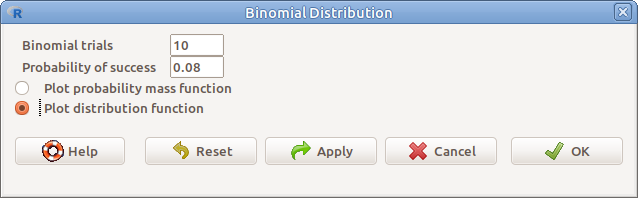
17.12: ábra Binomiális eloszlás ábrázolása: Distributions → Disctrete distributions → Binomial distribution → Plot binomial distribution

A függvények ábrázolásához a következőket kell megadni:

  • Binomial trials Kísérletek száma
  • Probability of success A bekövetkezés valószínűsége
  • Plot probability mass function Eloszlás
  • Plot distribution function Eloszlásfüggvény
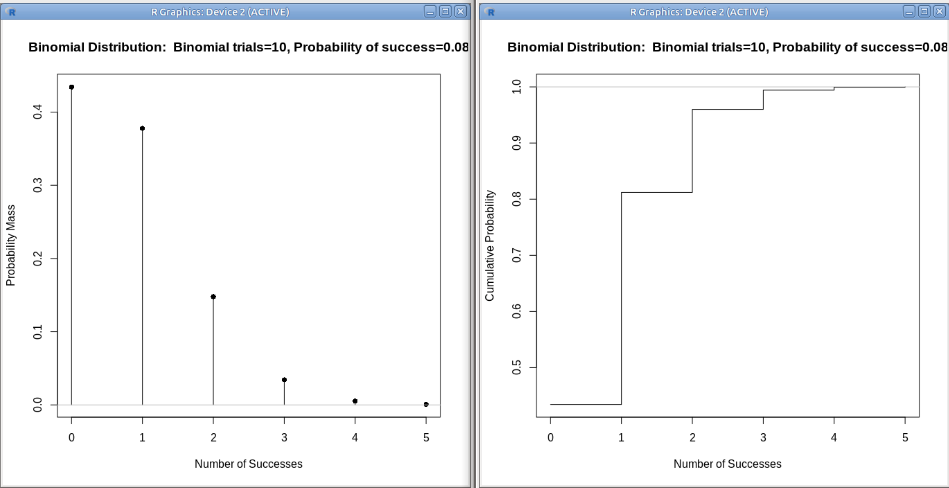
ábra Binomiális eloszlás (a) és eloszlásfüggvény (b)

17.13: ábra Binomiális eloszlás (a) és eloszlásfüggvény (b)

17.2.5 Mintavétel

Ezzel a lehetőséggel véletlen binomiális eloszlású mintákat készíthetünk. A mintaelemeket a mintaátlagokkal, szórásokkal, és a minta összegekkel együtt (ha bejelöljük) egy adattáblázatba írja bele a program, melyet menthetünk.

Megadandó:

  • Enter name of data set: Adattáblázat neve
  • Binomial trials Kísérletek száma
  • Probability of success A bekövetkezés valószínűsége
  • Number of samples (rows) Minták (sorok) száma
  • Number of observations (columns) Mintaelemek (oszlopok) száma mintánként
  • Add to Data Set Adattáblázatba kiírandó
    • Sample means Mintaátlagok
    • Sample sums Mintaelemek összege
    • Sample standard deviations Minta szórások
Mintavétel binomiális eloszlásból: *Distributions &rarr; Discrete distributions &rarr; Binomial distribution &rarr; Sample from binomial distribution*

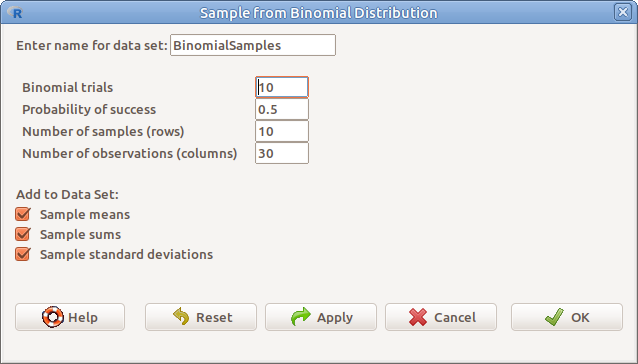
17.14: Mintavétel binomiális eloszlásból: Distributions → Discrete distributions → Binomial distribution → Sample from binomial distribution

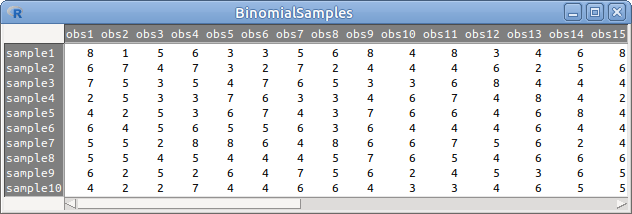
ábra Minták binomiális eloszlásból

17.15: ábra Minták binomiális eloszlásból

(TK. 3.5.1. fejezet 3.7. példa)