10 Hipotézisvizsgálatok: átlagok elemzése

Átlagok elemzésére szolgáló eljárásokat a Statistics → Means menüben találunk (10.1. ábra).

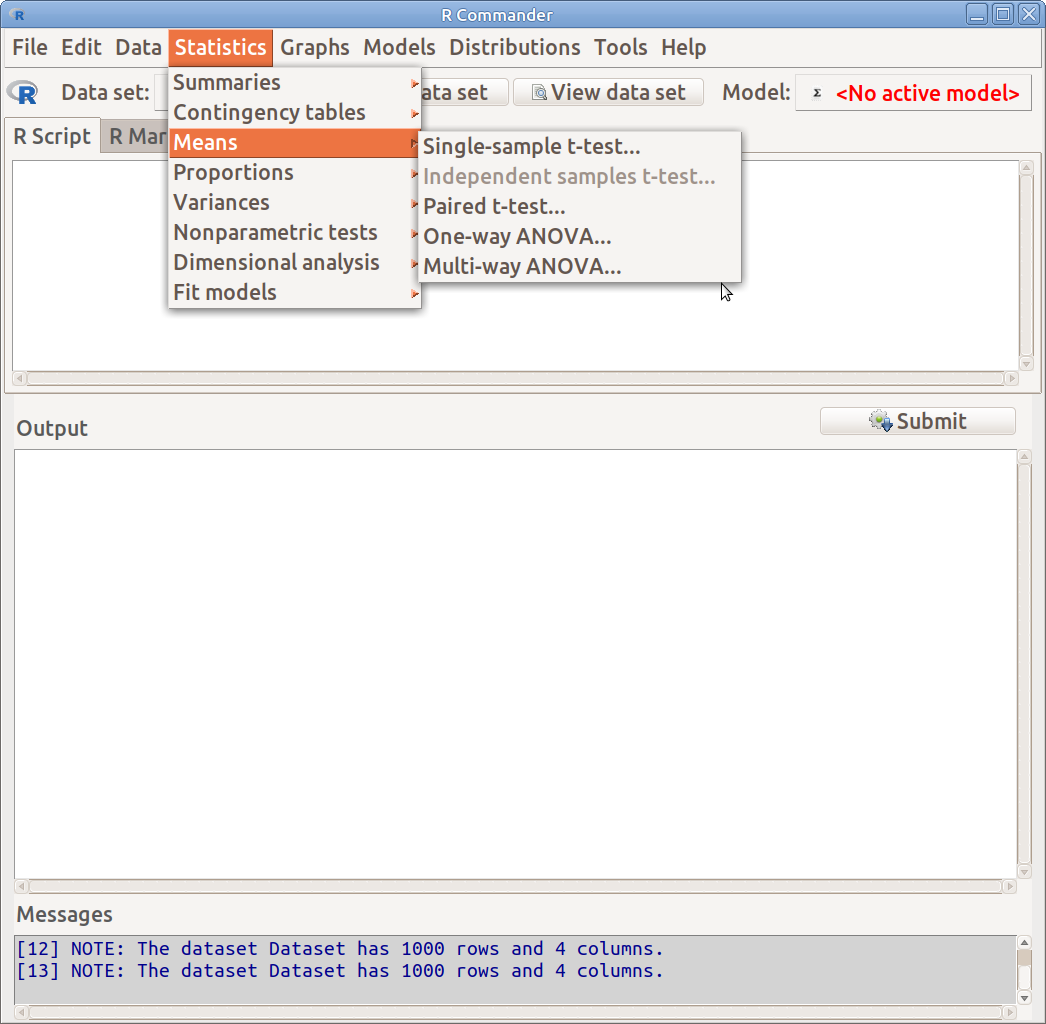
10.1: ábra Átlagok elemzése: Statistics → Means

10.1 Egymintás t-próba

Példánkban az vizsgáljuk egymintás t-próbával (Statistics → Means → Single sample t-test…), hogy az elsőéves hallgatók átlagos tömege szignifikánsan nagyobb-e, mint 78 kg (10.2. ábra). Ehhez meg kell adnunk a következőket:

Variable (pick one) A vizsgálandó változó
Alternative Hypothesis) Az ellenhipotézis típusa
- Population mean != mu0 \(H_1: \mu\neq \mu_0\)
- Population mean < mu0 \(H_1: \mu < \mu_0\)
- Population mean > mu0 \(H_1: \mu > \mu_0\)
Null hypothesis: mu = A tesztelendő hipotetikus érték (\(\mu_0\))
Confidence level A mintából becsült populáció átlagra vonatkozó konfidencia-intervallum megbízhatósági szintje

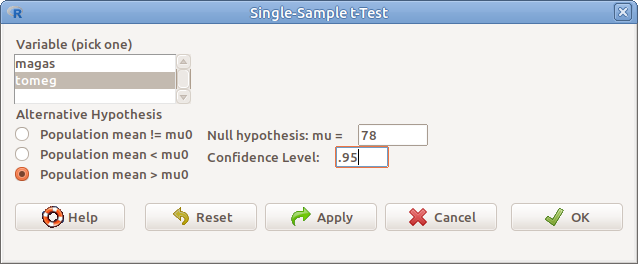
10.2: ábra Egymintás t-próba: Statistics → Means → Single sample t-test…

A teszt outputjában megkapjuk a \(t\)-statisztika értékét, a szabadsági fokot (df) és a p-értékek (p-value). Ezenkívül, kapunk egy – az alternatív hipotézis típusának megfelelő – konfidencia-intervallumot, valamint a mintaátlagot.

t.test(pop$tomeg, alternative='greater', mu=78, conf.level=.95)

## 
##  One Sample t-test
## 
## data:  pop$tomeg
## t = 5.238, df = 999, p-value = 9.895e-08
## alternative hypothesis: true mean is greater than 78
## 95 percent confidence interval:
##  79.24247      Inf
## sample estimates:
## mean of x 
##    79.812

(TK. 7.1.1. fejezet)

10.2 Két, független mintás t-próba

Példánkban az vizsgáljuk kétmintás t-próbával (Statistics → Means → Independent samples t-test…), hogy bizonyítják-e az alábbi minták, hogy a bikaborjak (b: bika) átlagos születéskori testtömege nagyobb, mint az üszőké (u: üsző). (10.3. ábra). Ehhez meg kell adnunk a következőket (borjak.csv).

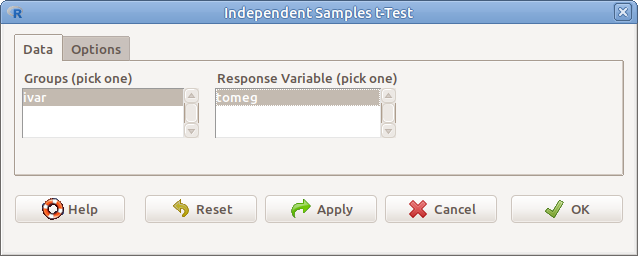
10.3: ábra Kétmintás t-próba: Statistics → Means → Independent samples t-test…

Groups (pick one) Csoportosító változó (2 szintű faktor lehet)
Response variable (pick one) A vizsgálandó változó

Az Options fülre kattintva a megjelenő párbeszéd ablakban (10.4. ábra) pedig a következőket:

Difference: b-u A különbség
Alternative Hypothesis - Two-sided \(H_1: \mu_1 - \mu_2 \neq 0\) - Difference < 0 \(H_1: \mu_1 - \mu_2 < 0\) - Difference > 0 \(H_1: \mu_1 - \mu_2 > 0\)
Confidence level A mintákból becsült, populációs átlagok különbségére vonatkozó konfidencia-intervallum megbízhatósági szintje.
Assume equal variances? Feltételezzük-e a populációs varianciák egyezőségét? Ha nem, No (alapbeállítás, hagyjuk így!), akkor a Welch-próbát végzi el a program.

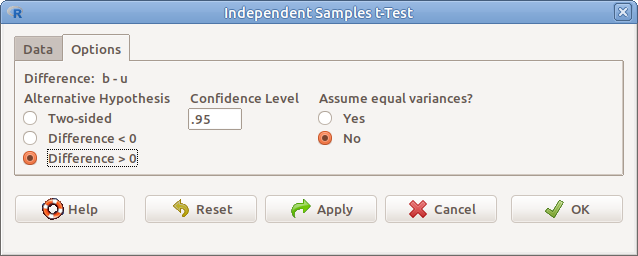
10.4: ábra Kétmintás t-próba: Statistics → Means → Independent samples t-test… → Options

A teszt outputjában megkapjuk a \(t\) statisztika értékét, a szabadsági fokot (df) és a \(p\)-értékek (p-value). Ezenkívül kapunk, egy – az alternatív hipotézis típusának megfelelő – konfidencia-intervallumot a populációs átlagok különbségére, valamint a mintaátlagokat.

t.test(tomeg~ivar, alternative='greater', conf.level=.95, var.equal=FALSE, data=borjak)

## 
##  Welch Two Sample t-test
## 
## data:  tomeg by ivar
## t = 0.99115, df = 11.736, p-value = 0.1708
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  -2.099368       Inf
## sample estimates:
## mean in group b mean in group u 
##        39.28571        36.66667

(TK. 7.1.2. fejezet, 7.2. példa)

10.3 Két, párosított mintás t-próba

Példánkban az vizsgáljuk páros t-próbával (Statistics → Means → Paired t-test…), hogy bizonyítják-e az adatok, hogy a második gyermek születéskori testtömege meghaladja az elsőét? (10.5. ábra, gyermek.csv). Ehhez meg kell adnunk a következőket:

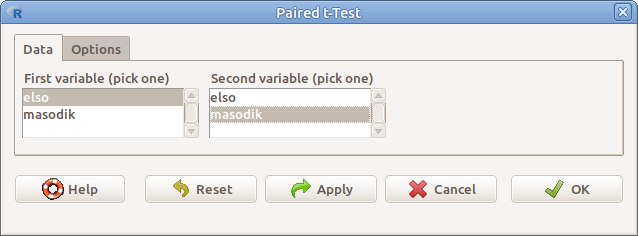
10.5: ábra Páros t-próba: Statistics → Means → Paired t-test…

First variable (pick one) Az egyik adatsort tartalmazó változó
Second variable (pick one) A másik adatsort tartalmazó változó

Az Options fülre kattintva a megjelenő párbeszéd ablakban pedig a következőket (10.6. ábra).

Alternative Hypothesis Alternatív hipotézis típusa - Two-sided \(H_1: \mu_1 - \mu_2 \neq 0\) - Difference < 0 \(H_1: \mu_1 - \mu_2 < 0\) - Difference > 0 \(H_1: \mu_1 - \mu_2 >0\)
Confidence level A mintákból becsült populációs átlagok különbségére vonatkozó konfidencia-intervallum megbízhatósági szintje.

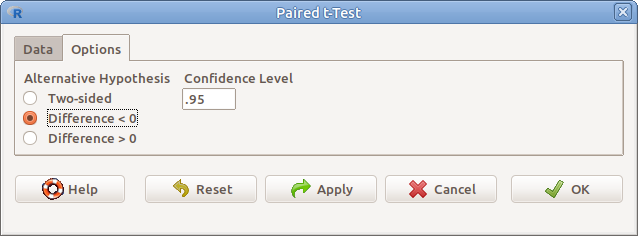
10.6: ábra Páros t-próba: Statistics → Means → Paired t-test… → Options

A teszt outputjában megkapjuk a \(t\)-statisztika értékét, a szabadsági fokot (df) és a \(p\)-értékek (p-value). Ezenkívül kapunk, egy – az alternatív hipotézis típusának megfelelő – konfidencia intervallumot a populációs átlagok különbségére, valamint a különbségek átlagát.

t.test(gyermek$elso, gyermek$masodik, alternative='less', conf.level=.95, paired=TRUE)

## 
##  Paired t-test
## 
## data:  gyermek$elso and gyermek$masodik
## t = -1.6692, df = 9, p-value = 0.06471
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##      -Inf 12.47327
## sample estimates:
## mean of the differences 
##                    -127

(TK. 7.1.3. fejezet, 7.3. példa)

10.3.1 10.4. Egytényezős ANOVA

Több átlag összehasonlítását varianciaelemzéssel végezzük el (Statistics → Means → One-way ANOVA…),. Példánkban egy kísérletben egy tápoldatot tesztelünk! A kísérletet 12 növénnyel végezzük, amelyek közül sorsolással eldöntjük, hogy melyik kapjon tiszta vizet, és melyiket öntözzük tömény, illetve híg oldattal. A növények magasságát vizsgáljuk. (tapoldat.csv). Az elemzéshez meg kell adnunk a következőket (@(ref(fig:egyanova). ábra).

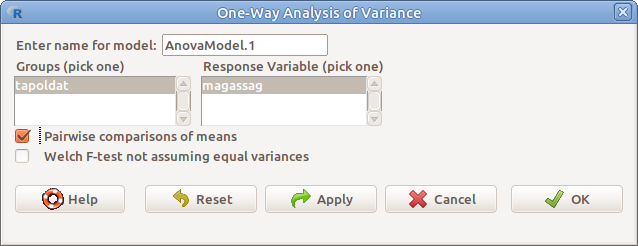
10.7: ábra Egytényezős ANOVA: Statistics → Means → One-way ANOVA…

Enter name of model: A modell elnevezése
Groups (pick one) Csoportosító változó
Response variable (pick one) A vizsgálandó célváltozó
Pairwise comparisons of means Páronkénti összehasonlítások elvégzése
Welch F-test not assuming equal variances A hagyományos F-teszt elvégzése helyett lehet végezni, ha nagyon különbözőek a varianciák. Nagy mintaelemszámok esetén jó megoldás.

A teszt outputjában megkapjuk az ANOVA-táblázatot a \(p\)-értékkel (Pr(>F)). Ezenkívül kapunk egy táblázatot a mintaátlagokkal, szórásokkal és mintaelemszámokkal.

AnovaModel.1 <- aov(magassag ~ tapoldat, data=adat)
summary(AnovaModel.1)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## tapoldat     2  303.5  151.75   18.84 0.000607 ***
## Residuals    9   72.5    8.06                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

numSummary(adat$magassag , groups=adat$tapoldat, statistics=c("mean", "sd"))

##         mean       sd data:n
## hig    56.75 1.258306      4
## tomeny 61.75 3.304038      4
## viz    49.50 3.415650      4

A páronkénti összehasonlítások eredményeként teszteket és konfidencia-intervallumokat kapunk a páronkénti különbségekre, a homogén csoportokat (ahol azonos betű van, azok a csoportátlagok nem különböznek szignifikánsan), valamint egy ábrát a különbségekkel és konfidencia-intervallumaikkal (10.8. ábra).

.Pairs <- glht(AnovaModel.1, linfct = mcp(tapoldat = "Tukey"))
summary(.Pairs) # pairwise tests

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: aov(formula = magassag ~ tapoldat, data = adat)
## 
## Linear Hypotheses:
##                   Estimate Std. Error t value Pr(>|t|)    
## tomeny - hig == 0    5.000      2.007   2.491   0.0798 .  
## viz - hig == 0      -7.250      2.007  -3.612   0.0139 *  
## viz - tomeny == 0  -12.250      2.007  -6.104   <0.001 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

confint(.Pairs) # confidence intervals

## 
##   Simultaneous Confidence Intervals
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: aov(formula = magassag ~ tapoldat, data = adat)
## 
## Quantile = 2.7888
## 95% family-wise confidence level
##  
## 
## Linear Hypotheses:
##                   Estimate lwr      upr     
## tomeny - hig == 0   5.0000  -0.5969  10.5969
## viz - hig == 0     -7.2500 -12.8469  -1.6531
## viz - tomeny == 0 -12.2500 -17.8469  -6.6531

cld(.Pairs) # compact letter display

##    hig tomeny    viz 
##    "b"    "b"    "a"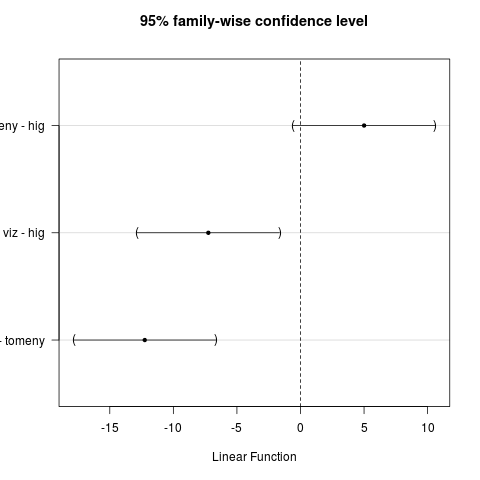

10.8: ábra Páronkénti különbségek konfidencia-intervallumokkal

(TK. 10.1. fejezet, 10.1.-2. példa)

10.4 Többtényezős ANOVA

Az előző fejezet tápoldatos kísérletet megismételték úgy is, hogy a szóban forgó növény két fajtáját kezelték az oldatokkal (tapoldat2.csv). A kiértékelést a többtényezős ANOVA elemzéssel végezzük el (Statistics → Means → Multi-way ANOVA…). (A fajta változót faktorrá kell alakítani!) Az elemzéshez meg kell adnunk a következőket (10.9. ábra).

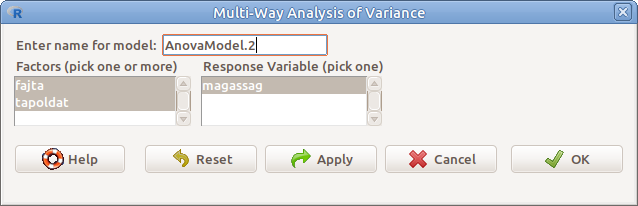
10.9: ábra Többtényezős ANOVA: Statistics → Means → Multi-way ANOVA…

Enter name of model: A modell elnevezése
Factors (pick one or more) Tényezők (faktorok)
Response variable (pick one) A vizsgálandó célváltozó

A teszt outputjában megkapjuk az ANOVA-táblázatot a \(p\)-értékekkel (Pr(>F)). Ezenkívül kapunk egy-egy táblázatot a kezelés kombinációnkénti mintaátlagokkal, szórásokkal és mintaelemszámokkal.

AnovaModel.2 <- (lm(magassag ~ fajta*tapoldat, data=adat2))
Anova(AnovaModel.2)

## Anova Table (Type II tests)
## 
## Response: magassag
##                Sum Sq Df F value    Pr(>F)    
## fajta           42.67  1  5.4857   0.03087 *  
## tapoldat       777.58  2 49.9875 4.481e-08 ***
## fajta:tapoldat  13.08  2  0.8411   0.44751    
## Residuals      140.00 18                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

tapply(adat2$magassag, list(fajta=adat2$fajta, tapoldat=adat2$tapoldat),
     mean, na.rm=TRUE) # means

##      tapoldat
## fajta   hig tomeny   viz
##     1 56.75  61.75 49.50
##     2 55.25  60.00 44.75

tapply(adat2$magassag, list(fajta=adat2$fajta, tapoldat=adat2$tapoldat),
    sd, na.rm=TRUE) # std. deviations

##      tapoldat
## fajta      hig   tomeny     viz
##     1 1.258306 3.304038 3.41565
##     2 3.403430 2.160247 2.50000

tapply(adat2$magassag, list(fajta=adat2$fajta, tapoldat=adat2$tapoldat),
    function(x) sum(!is.na(x))) # counts

##      tapoldat
## fajta hig tomeny viz
##     1   4      4   4
##     2   4      4   4

(TK. 10.3. fejezet, 10.3. példa)