9 Kontingencia-táblák elemzése

Kereszttábla, vagy más néven kontingencia-táblázatok elemzésére szolgáló eljárásokat a Statistics → Contingency tables menüben találunk (9.1. ábra).

9.1: ábra Kontingencia-táblázatok: Statistics → Contingency tables

Készíthetünk és elemezhetünk adattáblázatból kétdimenziós (Two-way table), többdimenziós táblázatot (Multi-way table), illetve elemezhetünk kézzel begépelt táblázatot (Enter and analyze two-way table…).

9.1 Kétdimenziós kontingencia-táblák elemzése

Kétdimenziós táblázat elemzéséhez meg kell adnunk a sorokba (Row variable (pick one)), illetve az oszlopokba kerülő faktor változót (Column variable (pick one)). Lehetőség van arra is, hogy a táblázatnak csak egy részére végezzük el az elemzéseket, ehhez 6. fejezetben leírt módon meg kell adni a résztáblázat eseteit meghatározó logikai kifejezést (9.2. ábra).

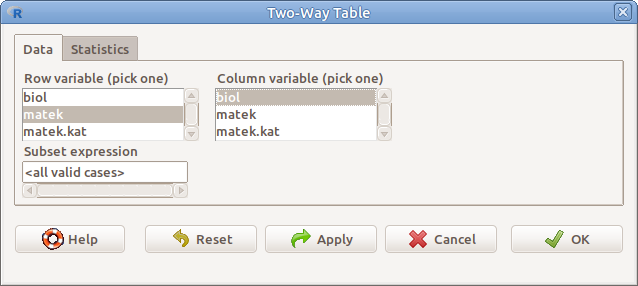
9.2: ábra Kétdimenziós kontingencia-táblák: Statistics → Contingency tables → Two-way table…

A változók megadása után a Statistics fülre kattintva beállíthatjuk, hogy milyen formában kérjük a kontingencia-táblát, illetve hogy milyen teszteket végezzen el a program (9.3. ábra).

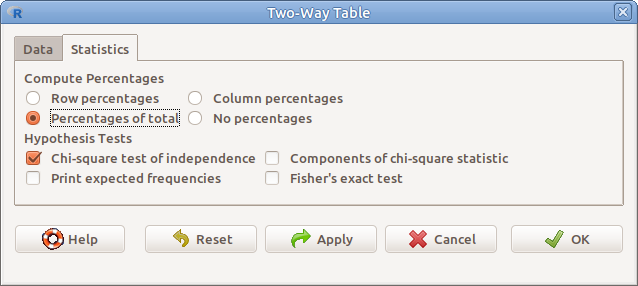
9.3: ábra Kontingencia-táblák készítése és elemzése: Statistics → Contingency tables → Two-way table… → Statistics

Compute Percentages Százalékos arányok
- Row percentages Soronkénti százalékos arányok
- Column percentages Oszloponkénti százalékos arányok
- Percentages of total Százalékos arányok az összgyakorisághoz képest
- No percentages Nem számol százalékos arányokat
Hypothesis Tests Függetlenségvizsgálatok
- Chi-square test of independence Khi-négyzet teszt
- Components of chi-square statistic A khi-négyzet statisztika komponensei
- Print expected frequencies Várt gyakoriságok kiíratása
- Fisher’s exact test Fisher-féle egzakt próba

A pop adattábla esetén, az output első részében a kontingencia-táblát láthatjuk, majd a megfelelő százalékos arányokat, végül a függetlenségvizsgálatok (esetünkben Khi-négyzet próba) eredményét. Az elemzés előtt a matek és biol változók faktorrá lettek alakítva.

.Table <- xtabs(~matek+biol, data=pop)
.Table

##      biol
## matek   1   2   3   4   5
##     1 121  55  56   0   0
##     2  80  38  43  37   0
##     3  42  29  40  32  45
##     4   0  43  39  40  69
##     5   0   0  40  35 116

totPercents(.Table) # Percentage of Total

##          1    2    3    4    5 Total
## 1     12.1  5.5  5.6  0.0  0.0  23.2
## 2      8.0  3.8  4.3  3.7  0.0  19.8
## 3      4.2  2.9  4.0  3.2  4.5  18.8
## 4      0.0  4.3  3.9  4.0  6.9  19.1
## 5      0.0  0.0  4.0  3.5 11.6  19.1
## Total 24.3 16.5 21.8 14.4 23.0 100.0

.Test <- chisq.test(.Table, correct=FALSE)
.Test

## 
##  Pearson's Chi-squared test
## 
## data:  .Table
## X-squared = 509.24, df = 16, p-value < 2.2e-16

(TK. 4.1.2. fejezet, 4.3. példa, 7.3.2. fejezet)

9.2 Többdimenziós táblázatok

Kettőnél több faktor változó esetén, a sor (Row variable), illetve oszlop változóként (Column variable) megjelölt változók kontingencia-tábláit a többi faktor változó (Control variables) kategóriái szerinti bontásban írathatjuk ki százalékos formában is (9.4. ábra).

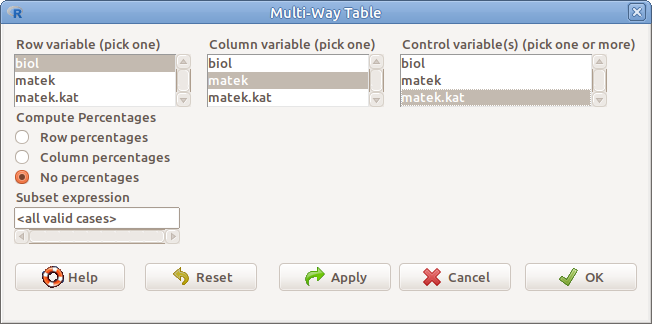
9.4: ábra Többdimenziós kontingencia-tábla: Statistics → Contingency tables → Multi-way table…

9.3 Kézzel begépelt kontingencia-tábla elemzése

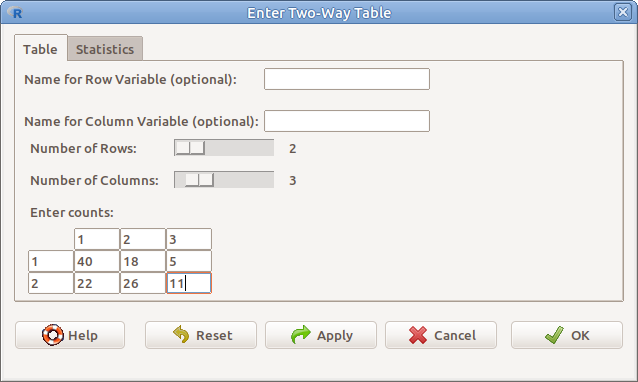
9.5: ábra Kétdimenziós kontingencia-tábla kézi bevitele: Statistics → Contingency tables → Enter and analyze two-way table…

Lehetőségünk van kézzel is begépelni kontingencia-táblát (9.5. ábra). Ehhez először be kell állítani a táblázat méretét, azaz a sorok számát (Number of Rows) és az oszlopok számát (Number of Columns), majd be kell gépelni a gyakoriságokat. Ezután a Statistics fülre kattintva be lehet állítani az előzőekhez hasonló százalékos arányokat, illetve teszteket (9.6. ábra).

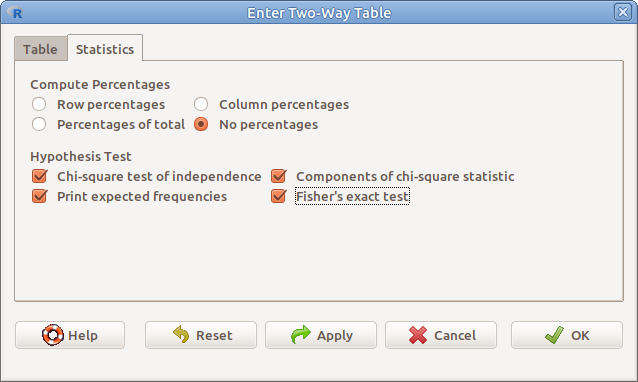
9.6: ábra Kézzel felvitt kétdimenziós tábla elemzési beállításai: Statistics → Contingency tables → Enter and analyze two-way table… → Statistics

A 9.6. ábrán látható beállításoknak megfelelő output első részében a kontingencia-táblát kapjuk meg, majd a Khi-négyzet teszt eredményét, utána a várt gyakoriságokat, majd a Khi-négyzet komponenseit, végül pedig a Fisher-próba eredményét.

.Table <- matrix(c(40,18,5,22,26,11), 2, 3, byrow=TRUE)
rownames(.Table) <- c('1', '2')
colnames(.Table) <- c('1', '2', '3')
.Table  # Counts

##    1  2  3
## 1 40 18  5
## 2 22 26 11

.Test <- chisq.test(.Table, correct=FALSE)
.Test

## 
##  Pearson's Chi-squared test
## 
## data:  .Table
## X-squared = 8.8087, df = 2, p-value = 0.01222

.Test$expected # Expected Counts

##          1        2        3
## 1 32.01639 22.72131 8.262295
## 2 29.98361 21.27869 7.737705

round(.Test$residuals^2, 2) # Chi-square Components

##      1    2    3
## 1 1.99 0.98 1.29
## 2 2.13 1.05 1.38

fisher.test(.Table)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  .Table
## p-value = 0.01073
## alternative hypothesis: two.sided

(TK. 7.3.2. fejezet, 7.6.- 7.10. példák)