14 Modellek illesztése
Különböző statisztikai modelleket a Statistics → Fit models menüben találunk (14.1. ábra). Lehetőség van lineáris regresszió (Linear regression), általános lineáris modell (Linear model), általánosított lineáris modell (Generalized linear model), polinomiális logit modell (Multinomial logit model) és ordinális regressziós modell (Ordinal regression model) illesztésére. Itt most a lineáris regressziós és az általános lineáris modell illesztését mutatjuk be.
14.1 Regressziószámítás
Regressziós modelleket vagy a Statistics → Fit models → Linear regression… vagy a Statistics → Fit models → Linear models… párbeszédablakban állíthatunk be (4. ábra). Mindkettő ugyanazt az lm() függvényt hívja meg, de míg az előbbiben csak numerikus magyarázó változókat adhatunk meg, addig ez utóbbiban faktorok is lehetnek.
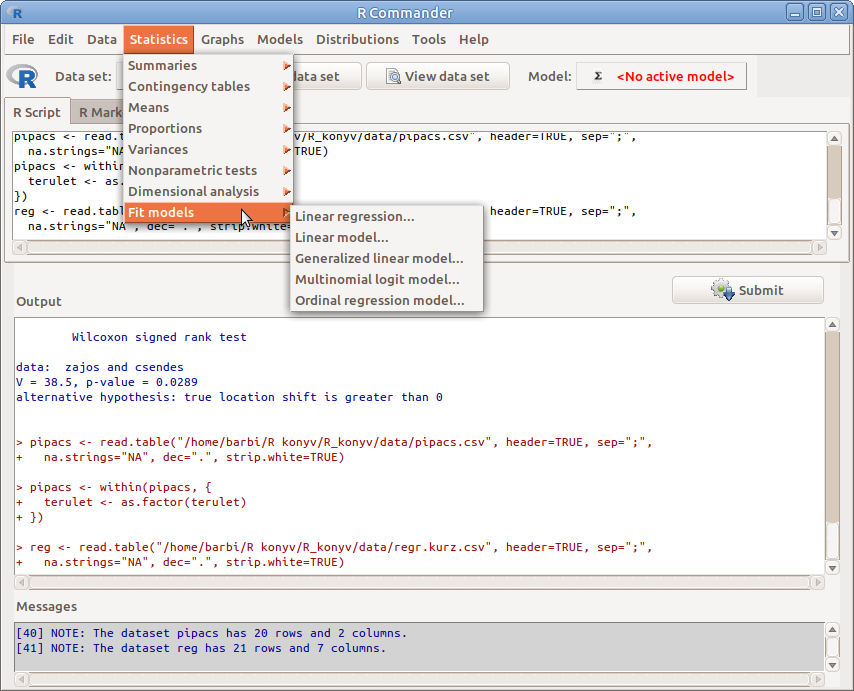
14.1: ábra Modellek illesztése: Statistics → Fit models
A regressziós kurzus példáján mutatjuk be a beállításokat (regr.kurz.csv). A testtömeg-születéskori tömeg adatokra végezzük el a regressziós elemzést. Az elemzéshez meg kell adnunk a következőket (14.2. ábra).
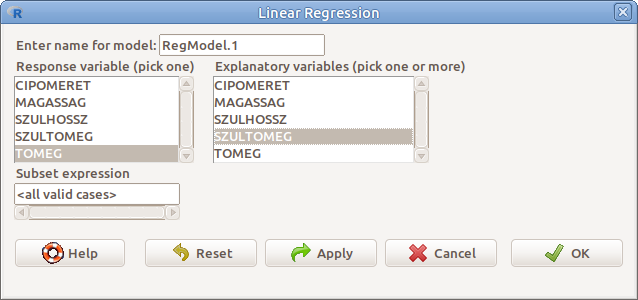
14.2: ábra Lineáris regresszió: Statistics → Fit models → Linear regression…
- Enter name of model: A modell elnevezése
- Response variable (pick one) Függő változó
- Explanatory variables (pick one or more) Magyarázó változó(k)
- Subset expression Rész adattáblázatot definiáló logikai kifejezés (ld. 6. fejezet)
A teszt outputjában megkapjuk a modell összegzését (summary): a reziduumokra vonatkozó statisztikákat (residuals), valamint a paraméterbecsléseket (Estimate), a becslések standard hibáit (Std. Error) és a \(t\)-próbák eredményeit (\(t\)- és \(p\)-értékek).
Az output utolsó részének első sorából kiderül, hogy mekkora a reziduumok
szórása (Residual standard error), és mekkora a szabadsági
foka (degrees of freedom). A második sorból olvashatjuk ki a determinációs együttható értékét (Multiple R-squared) és a korrigált determinációs együttható értékét (Adjusted R-squared)
Az utolsó sorban a modell egészére vonatkozó \(F\)-próba eredményét láthatjuk.
RegModel.1 <- lm(TOMEG~SZULTOMEG, data=regr.kurz)
summary(RegModel.1)##
## Call:
## lm(formula = TOMEG ~ SZULTOMEG, data = regr.kurz)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.0247 -7.1101 -0.7684 6.9753 18.4024
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.099147 14.380794 2.302 0.0328 *
## SZULTOMEG 0.009146 0.004029 2.270 0.0350 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.807 on 19 degrees of freedom
## Multiple R-squared: 0.2134, Adjusted R-squared: 0.172
## F-statistic: 5.153 on 1 and 19 DF, p-value: 0.03503(TK. 9.4. fejezet, 9.2.-3. példa)
14.2 A lineáris modell
Lineáris modelleket a Statistics → Fit models → Linear models párbeszédablakban állíthatunk fel (14.3. ábra). A példánkban lepkék bábtömegét (BABTOMEG) modellezzük a hőmérsékleti (HOM), a táplálékellátottság (TAP) kezelések, valamint a kezdeti hernyótömeg (TOMEG0) függvényében.
A párbeszédablakban a következőket kell beállítani:
- Enter name of model: A modell elnevezése
- Variables (double-click to formula) Az adattábla változói. A faktorok mögé szögletes zárójelben bekerül a factor szó. Dupla egér kattintással a modell formulába helyezhetők
- Model Formula A modell formula megadása (ld. alább)
- Subset expression Rész adattáblázatot definiáló logikai kifejezés (ld. 6. fejezet)
A modell formulába a változókat és operátorokat be lehet kézzel is írni, de a változó lista adott elemére dupla kattintással, illetve a megfelelő operátor gombokra kattintással is beletehetők. A bal oldalra kell a célváltozót írni. A jobb oldalra a magyarázó változókat a megfelelő operátorokkal összekapcsolva. Lehetőség van regressziós spline-ok és polinomiális tagok beillesztésére is (nem részletezzük).
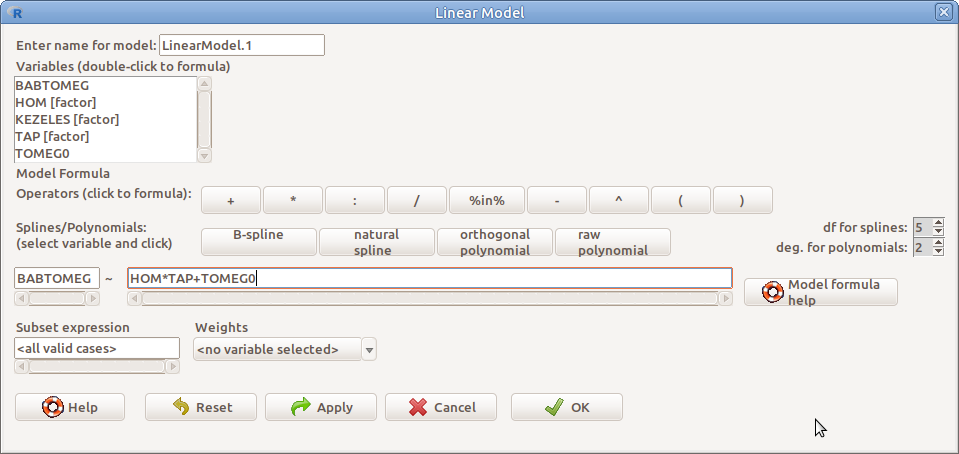
14.3: ábra Lineáris modell: Statistics → Fit models → Linear model…
Outputként a lineáris modell összegzését kapjuk meg. További modellekhez kapcsolódó műveletek (ANOVA-tábla, konfidencia-intervallumok, diagnosztika stb.) a Models menüben találhatók (ld. 16. fejezet).
LinearModel.1 <- lm(BABTOMEG ~ HOM*TAP +TOMEG0, data=lepke)
summary(LinearModel.1)##
## Call:
## lm(formula = BABTOMEG ~ HOM * TAP + TOMEG0, data = lepke)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.081285 -0.013193 0.002068 0.013066 0.057270
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.302322 0.009497 31.834 < 2e-16 ***
## HOMmelegitett 0.005363 0.012586 0.426 0.672
## HOMszobahom -0.003704 0.013808 -0.268 0.790
## TAPlimitalt -0.107056 0.014198 -7.540 9.7e-10 ***
## TOMEG0 0.189542 0.319718 0.593 0.556
## HOMmelegitett:TAPlimitalt -0.014198 0.018371 -0.773 0.443
## HOMszobahom:TAPlimitalt 0.010889 0.020064 0.543 0.590
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02898 on 49 degrees of freedom
## Multiple R-squared: 0.7977, Adjusted R-squared: 0.7729
## F-statistic: 32.2 on 6 and 49 DF, p-value: 2.176e-15(TK. o. 11.1.-5. fejezet)