11 Arányokra vonatkozó próbák

Arányokra (valószínűségekre) vonatkozó próbákat a Statistics → Proportions menüben találunk (11.1. ábra).

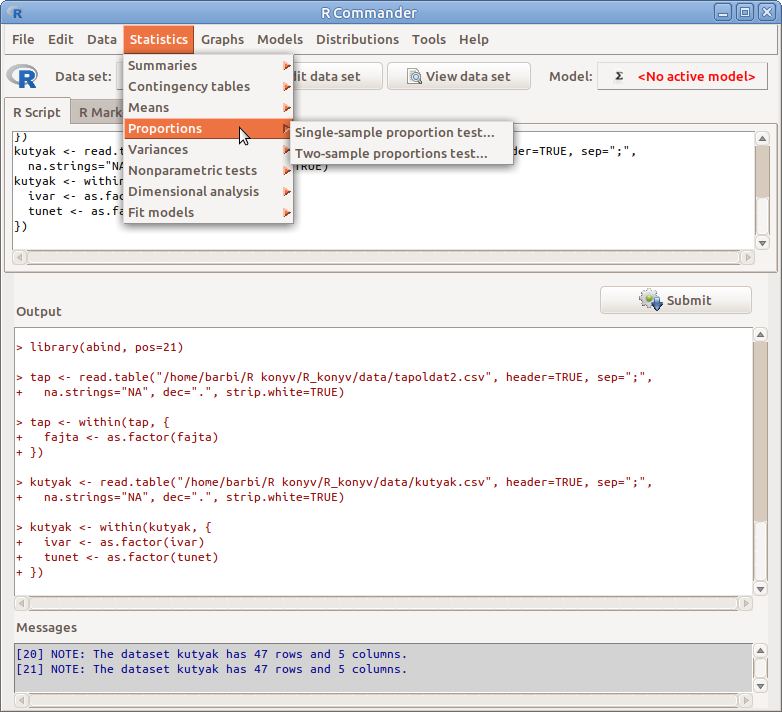
11.1: ábra Arányokra vonatkozó próbák: Statistics → Proportions

A próbák használatát egy olyan táblázat adatain keresztül mutatjuk be, amelyben kutyák adatai (kutyak.csv) vannak egy bizonyos betegség tüneteinek meglétéről (tunet, 0: nincs, 1: van), illetve a kutyák ivaráról (ivar, 0: hím, 1: szuka). Mindkét változót faktorrá kell alakítani az elemzés előtt. Mindkét faktor két szintű kell, hogy legyen.

11.1 Egy arány (valószínűség) vizsgálata

Vizsgáljuk meg először azt, hogy az ivararány megfelel-e az 1:1-es aránynak? Egzakt binomiális próbával végezzük el az elemzést. Ehhez meg kell adni a következőket (11.2. ábra):

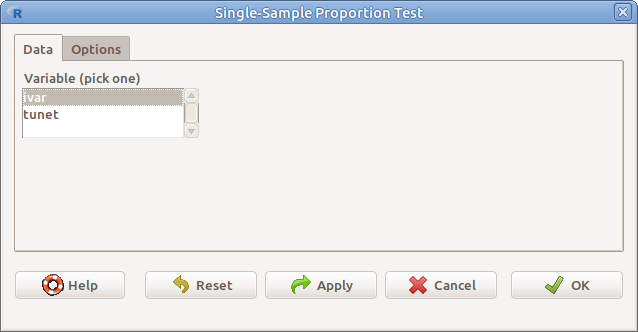
11.2: ábra Egy arány (valószínűség) vizsgálata: Statistics → Proportions → Single-sample proportion test…

• Variable (pick one) A vizsgálandó változó

Az Options fülre kattintva a megjelenő párbeszéd ablakban (11.3. ábra) pedig a következőket:

• Alternative Hypothesis Az alternatív hipotézis típusa
  • Population proportion != p0 \(H_1: p \neq p_0\)
  • Population proportion < p0 \(H_1: p < p_0\)
  • Population proportion > p0 \(H_1: p > p_0\)
• Type of test A teszt típusa
  • Normal approximation Normális közelítés korrekció nélkül
  • Normal approximation with continuity correction Normális közelítés folytonossági korrekcióval
  • Exact binomial Egzakt binomiális próba
• Null hypothesis: p = .5 A tesztelendő hipotetikus valószínűség (\(p_0\))
• Confidence Level A mintából becsült populációs arányra vonatkozó konfidencia-intervallum megbízhatósági szintje

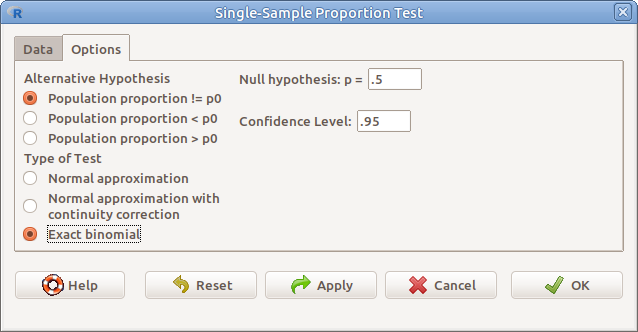
11.3: ábra Egy arány vizsgálatának beállításai: Statistics → Proportions → Single-sample proportion test… → Options

A teszt outputjában megkapjuk az ivarok gyakoriságait, a \(p\)-értéket (p-value). Ezenkívül kapunk egy – az alternatív hipotézis típusának megfelelő – konfidencia-intervallumot a populációs arányra, valamint az arány becslését.

.Table <- xtabs(~ ivar , data= kutyak )
.Table

## ivar
##  0  1 
## 22 25

binom.test(rbind(.Table), alternative='two.sided', p=.5, conf.level=.95)

## 
##  Exact binomial test
## 
## data:  rbind(.Table)
## number of successes = 22, number of trials = 47, p-value = 0.7709
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.3211153 0.6192221
## sample estimates:
## probability of success 
##              0.4680851

(TK. 7.4.1. fejezet)

11.2 Két arány hasonlítása független minták esetén

Példánkban azt vizsgáljuk, hogy a tünet előfordulási arány azonosnak tekinthető-e a hímek és szukák esetén. Korrekció nélküli normális közelítéssel végezzük el az elemzést. Ehhez meg kell adni a következőket (11.4. ábra):

11.4: ábra Két arány vizsgálata: Statistics → Proportions → Two-sample proportion test…

• Groups (pick one) Csoportosító változó
• Response variable (pick one) A vizsgálandó változó

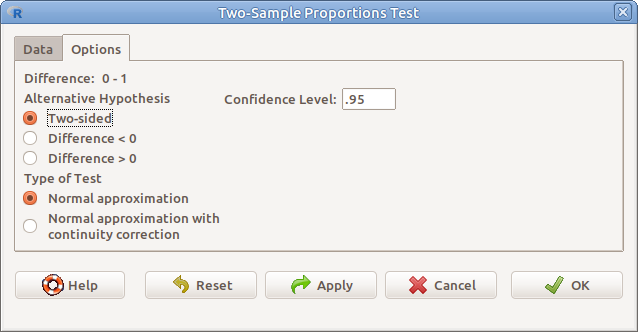
11.5: ábra Két arány összehasonlítása: Statistics → Proportions → Two-sample proportion test… → Options

Az Options fülre kattintva a megjelenő párbeszéd ablakban (@ref(fig.ketprop). ábra) pedig a következőket:

• Difference Különbség
• Alternative Hypothesis Az alternatív hipotézis típusa
  • Two-sided \(H_1: p_1 \neq p_2\)
  • Difference < 0 \(H_1: p_1 < p_2\)
  • Difference > 0 \(H_1: p_1 > p_2\)
• Type of test A teszt típusa
  • Normal approximation Normális közelítés korrekció nélkül
  • Normal approximation with continuity correction Normális közelítés folytonossági korrekcióval
• Confidence Level A mintából becsült populációs arányok különbségére vonatkozó konfidencia-intervallum megbízhatósági szintje

A teszt outputjában megkapjuk a tünet százalékos előfordulási arányát a két ivar esetén, valamint az ivarok gyakoriságait. A teszt outputjában megkapjuk a Khi-négyzet statisztika (X-squared) értékét, a szabadsági fokot (df), valamint a \(p\)-értéket (p-value). Ezenkívül kapunk egy – az alternatív hipotézis típusának megfelelő – konfidencia-intervallumot a populációs arányok különbségére, valamint az arányok becslését.

.Table <- xtabs(~ivar+tunet, data=kutyak)
rowPercents(.Table)

##     tunet
## ivar    0    1 Total Count
##    0 22.7 77.3   100    22
##    1 80.0 20.0   100    25

prop.test(.Table, alternative='two.sided', conf.level=.95, correct=FALSE)

## 
##  2-sample test for equality of proportions without continuity
##  correction
## 
## data:  .Table
## X-squared = 15.417, df = 1, p-value = 8.622e-05
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  -0.8077818 -0.3376728
## sample estimates:
##    prop 1    prop 2 
## 0.2272727 0.8000000

(TK. 7.4.2. fejezet)