13 Nemparaméteres próbák

Nemparaméteres próbákat a Statistics → Nonparametric tests menüben találunk (13.1. ábra).

13.1: ábra Nemparaméteres próbák: Statistics → Nonparametric tests

13.1 Két, független mintás Wilcoxon–Mann–Whitney próba

Példánkban azt vizsgáljuk egy kétmintás próbával (Statistics → Nonparametric tests → Two-samples Wilcoxon test…), hogy egy kísérletben, melyben enyhe vérszegénység vaskészítménnyel való kezelését tesztelték 10 kezelttel és 10 placebo-kontrollal, a kísérleti egyedeket a két csoportba véletlenszerűen besorolva, hogy a kezelt csoport hemoglobinszintje (g/dl) magasabb lett-e. A kontrollcsoportban az egyik mérés nem sikerült, ezért ott csak 9 érték van.? (13.2. ábra, hemoglobin.csv). Ehhez meg kell adnunk a következőket:

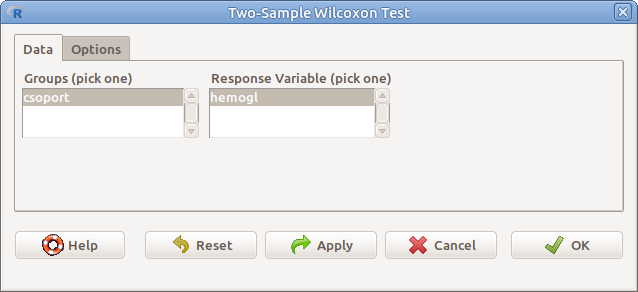
13.2: ábra Kétmintás Wilcoxon–Mann–Whitney próba: Statistics → Nonparametric tests → Two-samples Wilcoxon test…

• Groups (pick one) Csoportosító változó (2 szintű faktor lehet)
• Response variable (pick one) A vizsgálandó változó

Az Options fülre kattintva megjelenő párbeszéd ablakban (13.3. ábra) pedig a következőket:

• Difference Eltolás
• Alternative Hypothesis Az alternatív hipotézis típusa
  • Two-sided \(H_1:\) eltolás\(\neq 0\)
  • Difference < 0 \(H_1:\) eltolás\(<0\)
  • Difference > 0 \(H_1:\) eltolás\(>0\)
• Type of test A teszt típusa
  • Default Alapbeállítás
  • Exact Egzakt módszer
  • Normal approximation Normális közelítés korrekció nélkül
  • Normal approximation with continuity correction Normális közelítés folytonossági korrekcióval

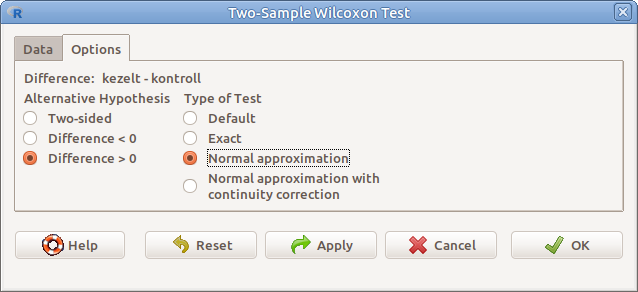
13.3: ábra Kétmintás Wilcoxon–Mann–Whitney próba: Statistics → Nonparametric tests → Two-samples Wilcoxon test… → Options

A teszt outputjában megkapjuk a minták mediánját, normális közelítést használva a \(W\) statisztika értékét és a \(p\)-értéket (p-value).

tapply(hemogl$hemogl, hemogl$csoport, median, na.rm=TRUE)

##   kezelt kontroll 
##    10.45     9.20

wilcox.test(hemogl ~ csoport, alternative='greater', exact=FALSE, correct=FALSE, data=hemogl)

## 
##  Wilcoxon rank sum test
## 
## data:  hemogl by csoport
## W = 76.5, p-value = 0.00499
## alternative hypothesis: true location shift is greater than 0

(TK. 7.6.2. fejezet, 7.18. példa)

13.2 Két, párosított mintás Wilcoxon–próba

Példánkban az vizsgáljuk egy páros próbával (Statistics → Nonparametric tests → Paired-samples Wilcoxon test…), hogy tíz kísérleti személynek ugyanazzal a módszerrel mérve a reakcióidejét csendes és zajos környezetben, bizonyíthatóan nagyobb-e a reakcióidő zajos környezetben? (13.4. ábra, reakcio_ido.csv). Ehhez meg kell adnunk a következőket:

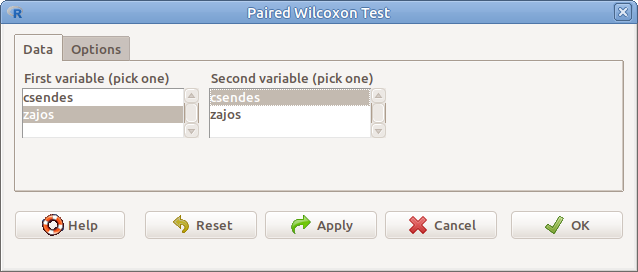
13.4: ábra Páros Wilcoxon–próba: Statistics → Nonparametric tests → Paired-samples Wilcoxon test…

• First variable (pick one) Egyik adatsort tartalmazó változó
• Second variable (pick one) Másik adatsort tartalmazó változó

Az Options fülre kattintva megjelenő párbeszéd ablakban (13.5. ábra) pedig a következőket:

• Alternative Hypothesis Az alternatív hipotézis típusa
  • Two-sided \(H_1:\) a különbségek mediánja\(\neq 0\)
  • Difference < 0 \(H_1:\) a különbségek mediánja\(<0\)
  • Difference > 0 \(H_1:\) a különbségek mediánja\(>0\)
• Type of test A teszt típusa
  • Default Alapbeállítás
  • Exact Egzakt módszer
  • Normal approximation Normális közelítés korrekció nélkül
  • Normal approximation with continuity correction Normális közelítés folytonossági korrekcióval

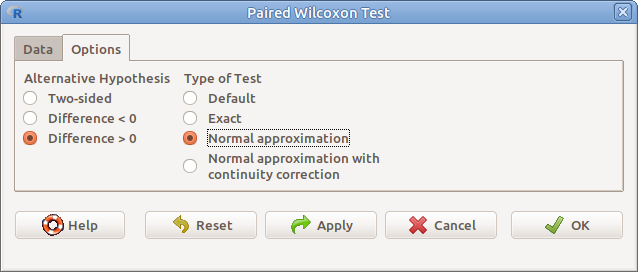
13.5: ábra Páros Wilcoxon–próba beállításai: Statistics → Nonparametric tests → Paired-samples Wilcoxon test… → Options

A teszt outputjában (normális közelítést használva) a \(W\) statisztika értékét és a \(p\)-értéket (p-value) kapjuk meg.

wilcox.test(reakcio$zajos, reakcio$csendes, alternative='greater', correct=FALSE, exact=FALSE, paired=TRUE)

## 
##  Wilcoxon signed rank test
## 
## data:  reakcio$zajos and reakcio$csendes
## V = 38.5, p-value = 0.0289
## alternative hypothesis: true location shift is greater than 0

(TK. 7.6.1. fejezet, 7.17 példa)

13.3 Több, független mintás Kruskal–Wallis-féle H-próba

Példánkban azt vizsgáljuk (Statistics → Nonparametric tests → Kruskal-Wallis test…), hogy négy terület mindegyikén 5-5 véletlenszerűen kiválasztott azonos méretű kvadrátban megszámolt pipacsok alapján, van-e különbség a négy terület között a pipacsok gyakoriságát tekintve. (@ref(fig.KW). ábra, pipacs.csv). Ehhez meg kell adnunk a következőket (a területet faktorrá kell alakítani):

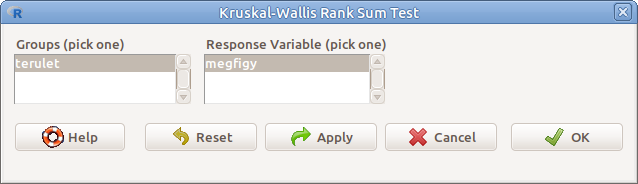
13.6: ábra Kruskal–Wallis-féle H-próba: Statistics → Nonparametric tests → Kruskal-Wallis test…

• Groups (pick one) Csoportosító változó (faktor!)
• Response variable (pick one) A vizsgálandó változó

A teszt outputjában megkapjuk a minta mediánokat, a Khi-négyzet statisztika (chi-squared) értékét a hozzá tartozó szabadsági fokkal (df) és a \(p\)-értéket (p-value).

tapply(pipacs$megfigy, pipacs$terulet, median, na.rm=TRUE)

##  1  2  3  4 
## 14 28  8 48

kruskal.test(megfigy ~ terulet, data=pipacs)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  megfigy by terulet
## Kruskal-Wallis chi-squared = 11.483, df = 3, p-value = 0.009381

(TK. 7.6.3. fejezet, 7.19. példa)

Ha ugyanazt a területet vizsgálnánk 4 különböző alkalommal, akkor a megfigyeléseink nem lennének függetlenek. Ekkor a menüben következő Friedman rank-sum test használata lehet alkalmas.