8 Leíró statisztikák

A leíró statisztikák kiszámítására szolgáló eljárásokat a Statistics → Summaries menüben találjuk (8.1. ábra).

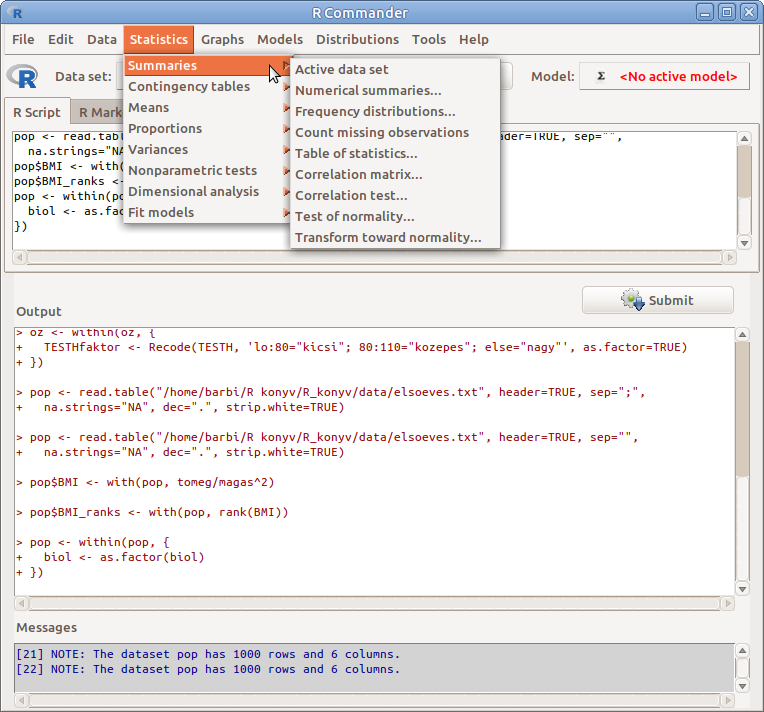
ábra Leíró statisztikák: *Statistics → Summaries*

8.1: ábra Leíró statisztikák: Statistics → Summaries

8.1 Aktív adattábla összegzése

Az aktív adattábla változóinak alapvető leíró statisztikáit írathatjuk ki (Statistics → Summaries → Active data set). Numerikus változók esetén a minimum (Min.), alsó kvartilis (1st Qu.), a medián (Median), az átlag (Mean), a felső kvartilis (3rd Qu.) és a maximum (Max.) értékeket. Faktor változók esetén pedig a kategóriák gyakoriságait.

summary(pop)
##      magas         tomeg            matek            biol      
##  Min.   :158   Min.   : 44.00   Min.   :1.000   Min.   :1.000  
##  1st Qu.:174   1st Qu.: 72.00   1st Qu.:2.000   1st Qu.:2.000  
##  Median :178   Median : 80.00   Median :3.000   Median :3.000  
##  Mean   :178   Mean   : 79.81   Mean   :2.911   Mean   :2.953  
##  3rd Qu.:182   3rd Qu.: 88.00   3rd Qu.:4.000   3rd Qu.:4.000  
##  Max.   :197   Max.   :112.00   Max.   :5.000   Max.   :5.000

8.2 Leíró statisztikák numerikus változókra

Az alapvető leíró statisztikákat a Statistics → Summaries → Numerical summaries… segítségével egy kategóriás változó kategóriáira bontva is kiszámíttathatjuk. A lepke táblázat TAP kategóriái esetén mutatjuk be a funkció használatát (8.2., 8.3., 8.4. ábrák). 8.2. ábrán látható ablakban kell kiválasztani a változó(ka)t, illetve a Summarize by groups gomb megnyomása után a kategóriás változót (8.3.. ábra). Ezután, rákattintva a Statistics gombra, kiválaszthatjuk a kiszámítandó statisztikákat (8.4. ábra):

  • Mean Átlag
  • Standard Deviation Szórás
  • Standard Error of Mean Átlagos hiba átlag
  • Interquartile Range Interkontinentilis terjedelem
  • Coefficient of Variation Relatív szórás v. variációs együttható
  • Binned Frequency Counts Gyakoriságok osztályintervallumokban a hisztogramnak megfelelően (15.3. fejezet)
  • Skewness Ferdeség
  • Kurtosis Csúcsosság
  • Quantiles Valószínűségek kvantilisekhez

(A ferdeséget és csúcsosságot nem szoktuk használni.)

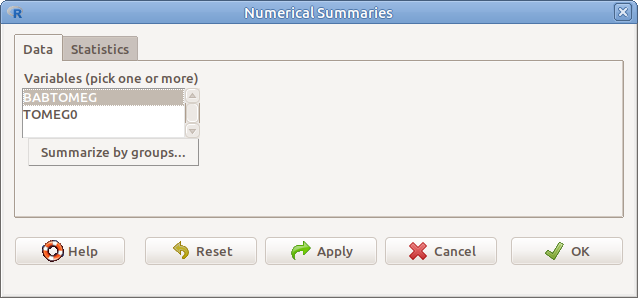
ábra Leíró statisztikák numerikus változókra: *Statistics → Summaries → Numerical summaries...*

8.2: ábra Leíró statisztikák numerikus változókra: Statistics → Summaries → Numerical summaries…

ábra Csoportok beállítása: *Statistics → Summaries → Numerical summaries... → Summarize by groups*

8.3: ábra Csoportok beállítása: Statistics → Summaries → Numerical summaries… → Summarize by groups

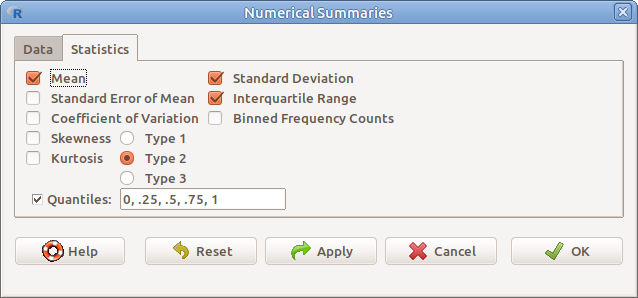
ábra Leíró statisztikák kiválasztása: *Statistics → Summaries → Numerical summaries... → Statistics*

8.4: ábra Leíró statisztikák kiválasztása: Statistics → Summaries → Numerical summaries… → Statistics

Az alábbi outputban az átlag (Mean), a szórás (sd), az interkvartilis terjedelem (IQR), a variációs együttható (cv), a kvartilisek (0%: minimum, 25%: alsó kvartilis, 50%: medián, 75%: felső kvartilis, 100%: maximum) és a kategóriák gyakoriságai (data:n) szerepelnek.

numSummary(lepke[,"BABTOMEG"], groups=lepke$TAP,
             statistics=c("mean", "sd", "IQR",  "quantiles", "cv"),
             quantiles=c(0,.25,.5,.75,1))
##                mean         sd     IQR         cv    0%    25%   50%
## adlibitum 0.3056667 0.02945404 0.02600 0.09635999 0.230 0.2915 0.309
## limitalt  0.1984231 0.02686138 0.03225 0.13537428 0.143 0.1830 0.195
##               75%  100% data:n
## adlibitum 0.31750 0.375     30
## limitalt  0.21525 0.252     26

(TK. 4.2. fejezet, 11.1.2. fejezet)

8.3 Gyakorisági eloszlások

Kategóriás (faktor, ha numerikusan kódolt, faktorrá kell először alakítani. ld. 7.3 fejezet) változók esetén gyakoriság táblázatot, illetve az eloszlás vizsgálatára szolgáló Khi-négyzet-próbát a Statistics → Summaries → Frequency distributions… párbeszédablak előhívásával írattathatunk ki, illetve végezhetünk (8.5. ábra). Ki kell választanunk a vizsgálandó változót (variables (pick one or more)). Ha Khi-négyzet próbát is szeretnénk végezni, akkor be kell jelölnünk a Chi-square goodness-of fit test (for one variable only) opciót.

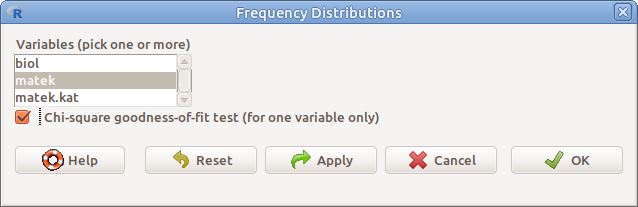
ábra Gyakorisági táblázat: *Statistics → Summaries → Frequency distributions*

8.5: ábra Gyakorisági táblázat: Statistics → Summaries → Frequency distributions

Az OK gomb megnyomása után felugró (8.6. ábra) meg kell adnunk az egyes kategóriákba tartozás hipotetikus valószínűségeit (alapbeállítás: egyenletes eloszlás).

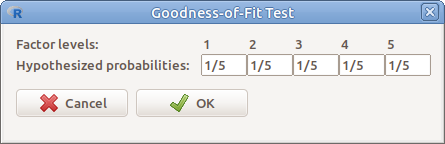
ábra Hipotetikus valószínűségek beállítása Khi-négyzet próbához: *Statistics → Summaries → Frequency distributions*

8.6: ábra Hipotetikus valószínűségek beállítása Khi-négyzet próbához: Statistics → Summaries → Frequency distributions

Az output első részébe a gyakoriságok, majd a százalékos gyakoriságok, végül a Khi-négyzet próba eredménye kerül kiíratásra.

.Table <- table(pop$matek)
.Table  # counts for matek
## 
##   1   2   3   4   5 
## 232 198 188 191 191
round(100*.Table/sum(.Table), 2)  # percentages for matek
## 
##    1    2    3    4    5 
## 23.2 19.8 18.8 19.1 19.1
.Probs <- c(0.2,0.2,0.2,0.2,0.2)
chisq.test(.Table, p=.Probs)
## 
##  Chi-squared test for given probabilities
## 
## data:  .Table
## X-squared = 6.67, df = 4, p-value = 0.1544

(TK. 2.4.2. fejezet 2.2. példa; 4.1.1. fejezet; 7.3.1. fejezet)

8.4 Hiányzó adatok száma

A Statistics → Summaries → Count missing observations opcióval az aktív táblázat hiányzó adatait számoltathatjuk meg változónként.

8.5 Leíró statisztikák két faktor szerinti bontásban

A leíró statisztikákat egyesével, két kategóriás változó szerinti bontásban is kiszámíttathatjuk (8.7. ábra). Be kell állítanunk a faktorokat (Factors (pick one or more)), illetve a numerikus változókat (Response variables (pick one or more)), valamint ki kell választanunk a statisztika típusát (Statistic).

ábra Leíró statisztikák táblázata: *Statistics &rarr; Summaries &rarr; Table of statistics... *

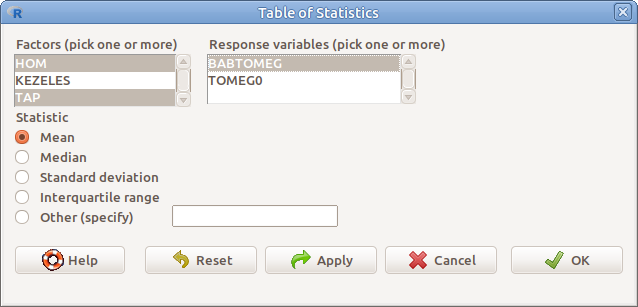
8.7: ábra Leíró statisztikák táblázata: Statistics → Summaries → Table of statistics… 

tapply(lepke$BABTOMEG, list(HOM=lepke$HOM, TAP=lepke$TAP), mean,
         na.rm=TRUE)
##             TAP
## HOM          adlibitum  limitalt
##   hutott     0.3038000 0.1996667
##   melegitett 0.3104167 0.1906000
##   szobahom   0.3008750 0.2080000

(TK. 11.1.2. fejezet)

8.6 Korrelációs mátrix

Korrelációs mátrix: *Statistics &rarr; Summaries &rarr; Correlation matrix... *

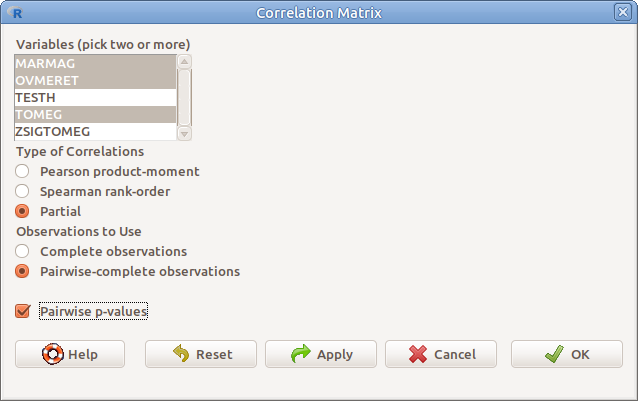
8.8: Korrelációs mátrix: Statistics → Summaries → Correlation matrix…

Több numerikus változó páronkénti Pearson, Spearman, illetve parciális korrelációját számíttathatjuk ki, illetve tesztelhetjük (kétoldali tesztek) a Statistics → Summaries → Correlation matrix funkcióval (8.8. ábra). Meg kell adnunk két, vagy több változót (Variables (pick two or more)), a korrelációs együttható típusát, valamint azt, hogy a hiányzó adatokat hogy kezelje a program (Observations to Use). A Complete observations lehetőség választása esetén, a program kihagyja az összes olyan esetet, amelyben bármelyik kiválasztott változó esetén adathiány van. Ha a Pairwise-complete observations lehetőséget választjuk, akkor minden változó pár esetén a lehető legtöbb adatot felhasználja, vagyis csak azokat hagyja el, amikben valamelyik változó esetén hiány van. A Pairwise p-values bejelölése esetén a korrelációkat teszteli is.

Az output első részében a korrelációs együtthatókat, majd a mintaelemszámokat, utána a korrelációs együttható tesztelésére kapott p-értékeket, majd a többszörös tesztelés miatt a Holm módszerrel korrigált p-értékeket Adjusted p-values (Holm’s method) láthatjuk.

partial.cor(ozmeret[,c("MARMAG","OVMERET","TOMEG")], tests=TRUE, use="pairwise.complete")
## 
##  Partial correlations:
##          MARMAG OVMERET   TOMEG
## MARMAG  0.00000 0.19510 0.52434
## OVMERET 0.19510 0.00000 0.50112
## TOMEG   0.52434 0.50112 0.00000
## 
##  Number of observations: 
##         MARMAG OVMERET TOMEG
## MARMAG     109     107   109
## OVMERET    107     107   107
## TOMEG      109     107   109
## 
##  Pairwise two-sided p-values:
##         MARMAG OVMERET TOMEG
## MARMAG         0.045   0.000
## OVMERET 0.045          0.000
## TOMEG   0.000  0.000        
## 
##  Adjusted p-values (Holm's method)
##         MARMAG OVMERET TOMEG
## MARMAG         0.045   0.000
## OVMERET 0.045          0.000
## TOMEG   0.000  0.000

(TK. 9.8.2. fejezet 9.10. példa, 8. fejezet)

8.7 Korrelációs együttható tesztelés

ábra Korreláció tesztelés: *Statistics &rarr; Summaries &rarr; Correlation test... *

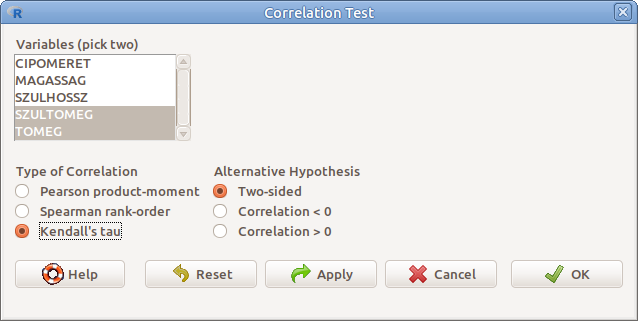
8.9: ábra Korreláció tesztelés: Statistics → Summaries → Correlation test…

Két változó Pearson-, Spearman- illetve Kendall-féle korrelációját tesztelhetjük. Egyoldali tesztek is végezhetők (8.9. ábra). Ehhez a következőket kell beállítani:

  • Variables (pick two) Változók kiválasztása
  • Type of Correlation A korrelációs együttható típusa
  • Alternative Hypothesis Az ellenhipotézis típusa
    • Two-sided \(H_1:\) Correlation \(\neq 0\)
    • Correlation<0 \(H_1:\) Correlation \(<0\)
    • Correlation>0 \(H_1:\) Correlation \(>0\)
cor.test(regr.kurz$SZULTOMEG, regr.kurz$TOMEG,
             alternative="two.sided", method="kendall")
## 
##  Kendall's rank correlation tau
## 
## data:  regr.kurz$SZULTOMEG and regr.kurz$TOMEG
## z = 2.3089, p-value = 0.02095
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
## 0.3725535

(TK. 8.2.1. fejezet 8.4. példa)

8.7.1 8.8. Normalitás tesztelése

Egy változó esetén végezhető el a Shapiro-Wilk-féle normalitás vizsgálat (Statistics → Summaries → Shapiro-Wilk test of normality…).