16 Modellekkel kapcsolatos műveletek
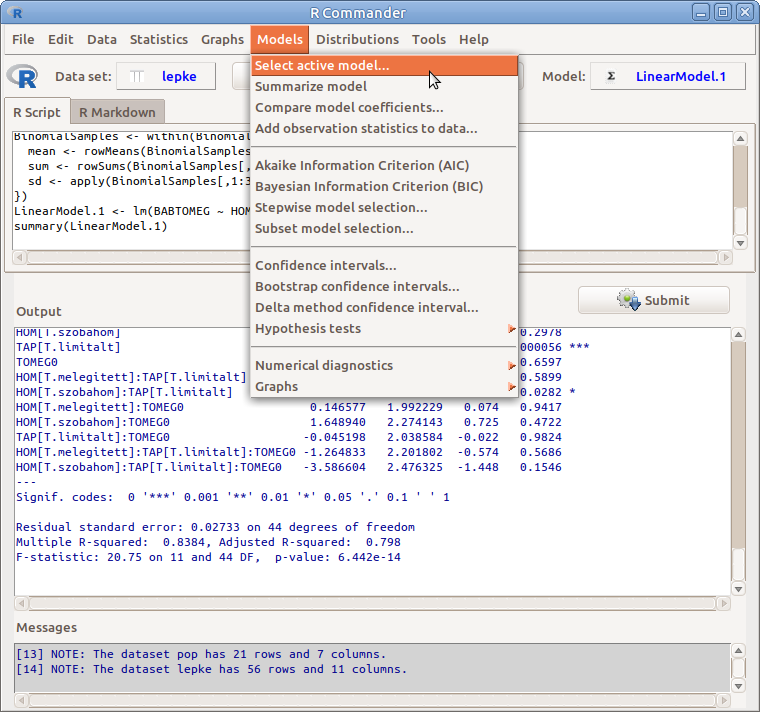
16.1: ábra Models menü: Models
Az éppen aktív modellel kapcsolatos műveleteket a Models menüben találunk (16.1. ábra). Mindig csak az aktuális modell típusnak megfelelő menüpontok elérhetők. Ebben a fejezetben a lineáris modellekhez kapcsolódó fontosabb lehetőségeket részletesen bemutatjuk, a többit csak felsorolásszerűen.
16.1 Az aktív modell kiválasztása
- Select active model… Az aktív modell általában az utoljára készített modell, de átállíthatjuk ezzel lehetőséggel, vagy az eszköztár jobb szélső – az éppen aktív modell nevét mutató – gombjának megnyomásával.
16.2 A modell összegzése
- Summarize model Az aktív modell összegzése:
summary()(ld. 14. fejezet output része). Lehetőség van különböző, ún. Sandwich estimator-ok választására a standard hiba becsléshez, amik jobb becslést adnak heteroscedasticitás illetve autokorreláció esetén.
(TK. 9.4.2. fejezet 9.3. példa)
16.3 Modellek együtthatóinak összehasonlítása
- Compare modell coefficients Két vagy több modell által becsült együtthatók és standard hibáinak kilistázása könnyebben összehasonlítható formában.
16.4 Modellből számított értékek
- Add observation statistics to data… Az adattáblához, új változókként hozzáfűzhetjük a következő, az aktív modellel számított értékeket (16.2. ábra):
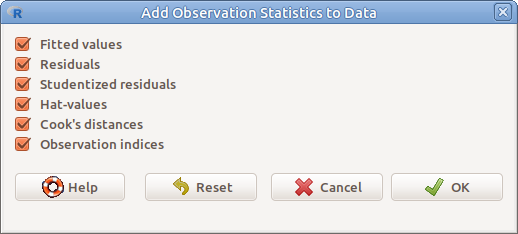
16.2: ábra Modellből számított értékek hozzáfűzése az adattáblázathoz: Models → Add observation statistics to data…
- Fitted values Becsült értékek
- Residuals Reziduumok
- Studentized residuals Studentizált (jacknife) reziduumok
- Hat-values Hatóerő értékek
- Cook’s distances Cook-féle távolságok
- Observation indices A megfigyelés sorszáma
(TK. 9.10.3. fejezet)
16.5 Infromációs kritériumok
- Akaike Information Criterion (AIC) A modell AIC értéke
- Bayesian Information Criterion (AIC) A modell BIC értéke
(TK. 11.7.3. fejezet 11.13. példa)
16.6 Lépésenkénti modellszelkeció
Lépésenkénti modellszelekció (Stepwise model selection). Megadandó a szelekció iránya (Direction) és az információs kritérium, ami alapján történik a szelekció (Criterion) (16.3. ábra).
Példánkban először létrehozzuk a következő modellt: BABTOMEG ~ TAP * HOM * TOMEG0. Majd elvégezzük a modellszelekciót.
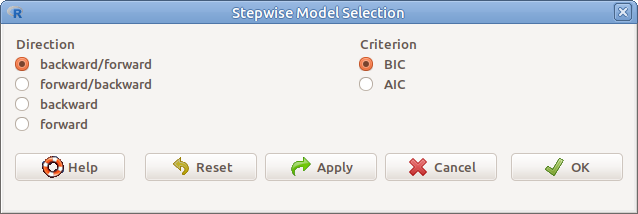
16.3: ábra Lépésenkénti modell szelekció: Models → Stepwise model selection…
Célszerű a futtatás után a szkript ablakban egy új modellt létrehozni (redmod) szelekció eredményeként, amellyel a továbbiakban dolgozhatunk:
LinearModel.2 <- lm(BABTOMEG ~ TAP*HOM*TOMEG0, data=lepke)
stepwise(LinearModel.2, direction='backward/forward', criterion='AIC')##
## Direction: backward/forward
## Criterion: AIC
##
## Start: AIC=-392.66
## BABTOMEG ~ TAP * HOM * TOMEG0
##
## Df Sum of Sq RSS AIC
## - TAP:HOM:TOMEG0 2 0.0020672 0.034941 -393.25
## <none> 0.032874 -392.66
##
## Step: AIC=-393.25
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:HOM + TAP:TOMEG0 + HOM:TOMEG0
##
## Df Sum of Sq RSS AIC
## - HOM:TOMEG0 2 0.0017574 0.036698 -394.50
## - TAP:HOM 2 0.0024081 0.037349 -393.52
## <none> 0.034941 -393.25
## + TAP:HOM:TOMEG0 2 0.0020672 0.032874 -392.66
## - TAP:TOMEG0 1 0.0047721 0.039713 -388.08
##
## Step: AIC=-394.5
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:HOM + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## - TAP:HOM 2 0.0015089 0.038207 -396.24
## <none> 0.036698 -394.50
## + HOM:TOMEG0 2 0.0017574 0.034941 -393.25
## - TAP:TOMEG0 1 0.0044463 0.041145 -390.10
##
## Step: AIC=-396.24
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## - HOM 2 0.0003650 0.038572 -399.71
## <none> 0.038207 -396.24
## + TAP:HOM 2 0.0015089 0.036698 -394.50
## + HOM:TOMEG0 2 0.0008582 0.037349 -393.52
## - TAP:TOMEG0 1 0.0043408 0.042548 -392.22
##
## Step: AIC=-399.71
## BABTOMEG ~ TAP + TOMEG0 + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## <none> 0.038572 -399.71
## + HOM 2 0.0003650 0.038207 -396.24
## - TAP:TOMEG0 1 0.0040274 0.042600 -396.15##
## Call:
## lm(formula = BABTOMEG ~ TAP + TOMEG0 + TAP:TOMEG0, data = lepke)
##
## Coefficients:
## (Intercept) TAPlimitalt TOMEG0
## 0.29166 -0.08775 1.21381
## TAPlimitalt:TOMEG0
## -1.43854redmod = stepwise(LinearModel.2, direction='backward/forward', criterion='AIC')##
## Direction: backward/forward
## Criterion: AIC
##
## Start: AIC=-392.66
## BABTOMEG ~ TAP * HOM * TOMEG0
##
## Df Sum of Sq RSS AIC
## - TAP:HOM:TOMEG0 2 0.0020672 0.034941 -393.25
## <none> 0.032874 -392.66
##
## Step: AIC=-393.25
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:HOM + TAP:TOMEG0 + HOM:TOMEG0
##
## Df Sum of Sq RSS AIC
## - HOM:TOMEG0 2 0.0017574 0.036698 -394.50
## - TAP:HOM 2 0.0024081 0.037349 -393.52
## <none> 0.034941 -393.25
## + TAP:HOM:TOMEG0 2 0.0020672 0.032874 -392.66
## - TAP:TOMEG0 1 0.0047721 0.039713 -388.08
##
## Step: AIC=-394.5
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:HOM + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## - TAP:HOM 2 0.0015089 0.038207 -396.24
## <none> 0.036698 -394.50
## + HOM:TOMEG0 2 0.0017574 0.034941 -393.25
## - TAP:TOMEG0 1 0.0044463 0.041145 -390.10
##
## Step: AIC=-396.24
## BABTOMEG ~ TAP + HOM + TOMEG0 + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## - HOM 2 0.0003650 0.038572 -399.71
## <none> 0.038207 -396.24
## + TAP:HOM 2 0.0015089 0.036698 -394.50
## + HOM:TOMEG0 2 0.0008582 0.037349 -393.52
## - TAP:TOMEG0 1 0.0043408 0.042548 -392.22
##
## Step: AIC=-399.71
## BABTOMEG ~ TAP + TOMEG0 + TAP:TOMEG0
##
## Df Sum of Sq RSS AIC
## <none> 0.038572 -399.71
## + HOM 2 0.0003650 0.038207 -396.24
## - TAP:TOMEG0 1 0.0040274 0.042600 -396.15A redukált modell összegzése (Summarize model):
summary(redmod, cor=FALSE)##
## Call:
## lm(formula = BABTOMEG ~ TAP + TOMEG0 + TAP:TOMEG0, data = lepke)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.084718 -0.016629 -0.001001 0.017550 0.055207
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.291655 0.007637 38.190 < 2e-16 ***
## TAPlimitalt -0.087752 0.012789 -6.862 8.23e-09 ***
## TOMEG0 1.213812 0.502142 2.417 0.0192 *
## TAPlimitalt:TOMEG0 -1.438542 0.617372 -2.330 0.0237 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02724 on 52 degrees of freedom
## Multiple R-squared: 0.8104, Adjusted R-squared: 0.7994
## F-statistic: 74.07 on 3 and 52 DF, p-value: < 2.2e-16(TK. 11.8. fejezet 11.14. példa)
16.7 Részmodell kiválasztása
A Subset model selection Egy olyan ábrát produkál, amelyen különböző paraméterszámú részmodelleket lehet összehasonlítani különböző, a modell “jóságát” mérő értékek alapján.
16.8 Konfidencia-intervallumok
Az adott modell együtthatóira számoltathatunk különböző konfidencia-intervallumokat, a szokásos standard hibán és t-eloszláson alapulót (Models → Confidence intervals…), bootstrap konfidencia-intervallumot, illetve a delta módszeren alapulót is. A konfidencia szint állítható (Confidence level).
(TK. 9.4.3. fejezet, 11.5.5. fejezet 11.10. példa)
16.9 Hipotézis vizsgálatok
A modellel kapcsolatos hipotézisvizsgálatok (16.4. ábra).
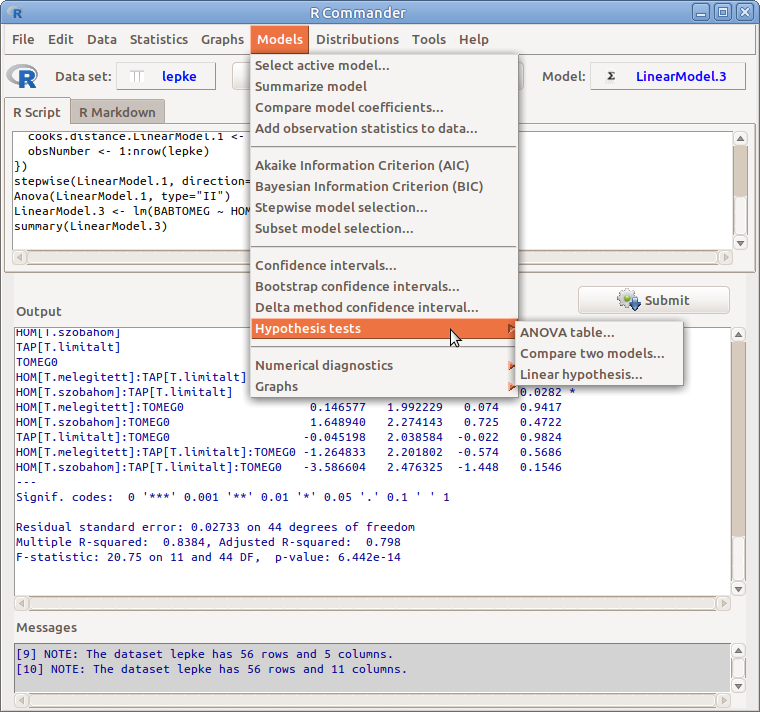
16.4: ábra Hipotézisvizsgálatok: Models → Hypothesis tests
16.9.1 ANOVA-tábla
A modell ANOVA-táblázatát írja ki. Meg lehet adni, hogy melyik négyzetösszeggel, illetve “Sandwich estimator”-ral számoljon (16.5. ábra). (Megjegyzés: Nem az R anova() függvényét hívja meg, hanem a car csomag Anova() függvényét!).
16.5: ábra Négyzetösszeg típusának kiválasztása: Models → Hypothesis tests → ANOVA table
A modellszelekcióval redukált modell ANOVA-táblája II-es típusú négyzetösszeggel számolva:
Anova(redmod, type="II")## Anova Table (Type II tests)
##
## Response: BABTOMEG
## Sum Sq Df F value Pr(>F)
## TAP 0.134792 1 181.7155 < 2e-16 ***
## TOMEG0 0.000597 1 0.8053 0.37366
## TAP:TOMEG0 0.004027 1 5.4294 0.02372 *
## Residuals 0.038572 52
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1(TK. 11.5.3. fejezet 11.8. példa)
16.9.2 Modellek összehasonlítása
Két beágyazott modell összehasonlítása F-teszttel. Ki kell választani a megjelenő párbeszédablakban az összehasonlítandó modelleket ((fig:modoh). ábra).

16.6: ábra Modellek összehasonlítása: Models → Hypothesis tests → Compare two models…
anova(LinearModel.2, redmod)## Analysis of Variance Table
##
## Model 1: BABTOMEG ~ TAP * HOM * TOMEG0
## Model 2: BABTOMEG ~ TAP + TOMEG0 + TAP:TOMEG0
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 44 0.032874
## 2 52 0.038572 -8 -0.0056984 0.9534 0.4839(TK. 11.5.3. fejezet 11.7. példa, 11.14. példa)
16.9.3 Lineáris hipotézisek tesztelése
Ebben a pontban van lehetőség arra, hogy a modellben kontrasztokat (a modellparaméterekből képzett lineáris kombináció) teszteljünk.
(TK. 11.11. fejezet)
16.10 Diagnosztikai eszközök
Lehetőség van numerikus és grafikus modelldiagnosztikák készítésére. Ezek közül csak a legáltalánosabban használtakat részletezzük.
16.10.1 Numerikus diagnosztikák
A modell változóinak általánosított variancia infláció faktorát a Models → Numerical diagnostics → Variance-inflation factors választásával számíttathatjuk ki. A többi lehetőséggel tesztelhetjük a hibatag szórásának állandóságát, az autókorreláltságot, nemlinearitást, kiugró értékeket, illetve transzformálhatjuk a célváltozót.
(TK. 278. o. 9.9. fejezet 9.11. példa)
16.10.2 Grafikus diagnosztikák
A szokásos diagnosztikus ábrákat a Models → Graphs → Basic diagnostic plots pontban találjuk (16.7. ábra).
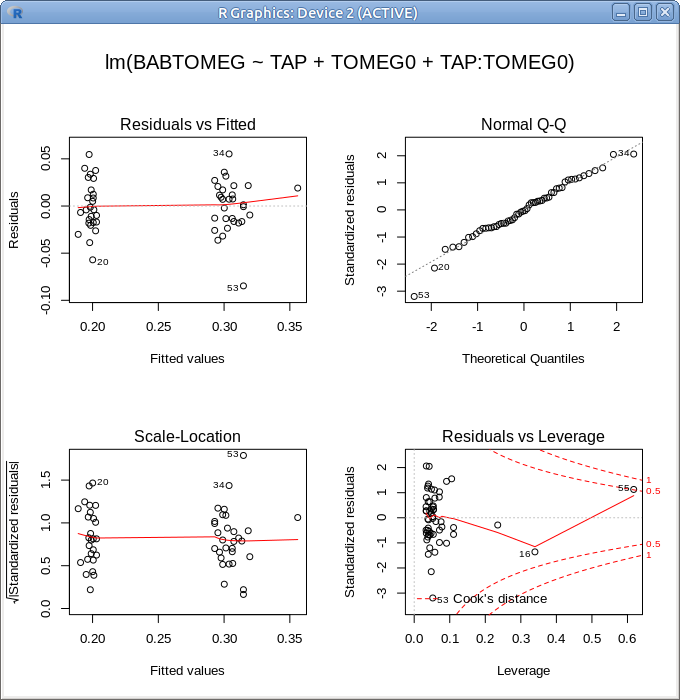
16.7: ábra Diagnosztikus ábrák: Models → Graphs → Basic diagnostic plots
(TK. 9.10.4. fejezet 9.20. ábra, 11.6. fejezet 11.11. példa)