2 A statisztika alapfogalmai
A statisztika adatgyűjtéssel, majd a megfigyelt adatok lényegre törő ábrázolásával, illetve elemzésével foglalkozik (Armitage, Berry, and Matthews (2008), Freedman et al. (2005)). Az elemzések célja a konkrét, egyedi megfigyelésekből általánosabb érvényű következtetések levonása. A következőkben összefoglaljuk azokat a legfontosabb fogalmakat és elnevezéseket, amelyekre a további fejezetekben építeni fogunk, és amelyek az irodalom értő olvasásához is nélkülözhetetlenek.
Biológusok, figyelem! A populáció elnevezés a statisztikában is használatos, de más a jelentése, mint a biológiában (lásd alább). Ebben a könyvben populáció alatt statisztikai populációt értünk (ha valahol mégsem, akkor ott mindig kiírjuk, hogy ,,biológiai populáció’’).
2.1 Populáció és minta
Ahhoz, hogy a populáció és a minta fogalmát megértsük, először a megfigyelési egység fogalmát kell tisztáznunk. Egy megfigyelési egység vagy mintavételi egység (observational unit, sampling unit, subject) a vizsgálat alanya vagy tárgya, amelyen a méréseket, vizsgálatokat végezzük. Megfigyelési egység lehet egy Petri-csésze, egy vérminta, egy sejtcsoport, egy szerv, egy 20 négyzetméteres mintaterület, egy 1 hektáros erdőrészlet, egy faj, egy egyed, egy nyáj, egy ember, egy család, egy iskolai osztály, egy iskola, egy választókerület, egy település stb.
A megfigyelési egységek választásban az is szerepet játszik, hogy egyáltalán mi vizsgálható, mi milyen pontossággal mérhető stb. Természetesen a megfigyelési egységek megválasztásától függően a megfigyelt adatok is változhatnak. Például baromfi takarmányozási kísérletekben tipikus, hogy a súlygyarapodás állatonként mérhető, de a takarmányfogyasztás csak ketrecenként, egyedenként nem. Most vajon az egyedi állatot vagy a ketrecet tekintsük a megfigyelési egységnek? Ha az egyedi állatot, akkor a takarmányfogyasztását jellemezhetjük az egy állatra jutó átlagos takarmányfogyasztással (azaz azt feltételezzük, hogy ugyanabban a ketrecben minden állat azonos mennyiséget fogyasztott), ha pedig a ketrecet, akkor a ketrecbeli átlagos súlygyarapodást érthetjük súlygyarapodás alatt.
Ha kell, megtehetjük azt is, hogy ugyanazon adatok egyik elemzésében mást tekintünk megfigyelési egységnek, mint egy másikban. Vérparaméterek vizsgálatakor például elképzelhető, hogy minden állatból azonos időpontban 3 vérmintát veszünk, mert azt is szeretnénk látni, hogy milyen pontossággal ismételhető a mérés. Kérdés, hogy most mit tekintsünk megfigyelési egységnek, egy vérmintát vagy egy állatot, azaz 3 összetartozó vérmintát? Választhatunk: ha elsősorban a mérés ismételhetősége érdekel, akkor a vérmintát, ha pedig az állatok állapota, akkor az állatot, amely ekkor jellemezhető a három mért adat átlagával (mert az átlag pontosabb, mint bármelyik egyedi mérés). Ha ez is, az is, végezhetünk két elemzést, egyiket így, másikat úgy.
Vagy tegyük fel, hogy madárfészkeket számolunk sok 1-1 hektáros erdőrészletben, emellett minden fészekben megszámoljuk a lerakott tojásokat is. Az így gyűjtött adatokat felfoghatjuk úgy, hogy a megfigyelési egység az erdőrészlet, így minden erdőrészlethez van két adatunk, a fészkek száma és a tojások össz-száma. Ugyanakkor gondolhatjuk úgy is, hogy a megfigyelési egység a fészek, így minden fészekhez tartozik két adat, a tojások száma és az erdőrészlet sorszáma, amelybe a fészek esik.
Már a fenti példák alapján is nyilvánvaló: nem mindegy, mit választunk megfigyelési egységnek, hiszen már a mintanagyság is különböző egyik vagy másik esetben. A választás azt is meghatározhatja, hogy mely statisztikai módszereket alkalmazhatjuk, sőt a módszerek alkalmazhatósági feltételei is eltérőek lehetnek.
A minta (sample) a ténylegesen megvizsgált, illetve vizsgálatra kiválasztott megfigyelési egységek halmaza, míg a populáció vagy alapsokaság (population) az összes lehetséges, szóba jöhető mintavételi egységet tartalmazó halmaz}, amelynek a minta részhalmaza.
Valójában mindig a populáció az a kör, amelyre a vizsgálat irányul, amelyre eredményeinket, következtetéseinket vonatkoztatni szeretnénk.
A populáció gyakran egy konkrét, jól meghatározott, véges halmaz – például egy tehenészetbeli összesen 355 tehén –, de ez nem mindig van így. Például egy, az allergiás bőrtüneteket enyhítő szerrel kapcsolatban beszélhetünk az ,,allergiás bőrtüneteket mutatókról’‘, akikre a szer hatását vizsgálni szeretnénk. Ezt ,,képzetes populációnak’‘, ,,végtelen populációnak’’ vagy ,,hipotetikus populációnak’’ is szokták nevezni, mivel beleértjük azokat is, akik bárhol a világban, és bármikor – esetleg csak a jövőben – jelentkeznek majd bőrtünetekkel. Végtelen populációból származó számszerű megfigyeléseket a valószínűségszámításban a valószínűségi változó fogalmával modellezünk ??. fejezetben.
Vigyázzunk, hogy ne okozzon félreértéseket, ha egy vizsgálatban más a statisztikai és más a biológiai populáció! A fenti – madárfészkek számlálásáról szóló – példában a biológiai populációt a madarak, a statisztikai populációt pedig az erdőrészletek (vagy a fészkek) alkotják. Általában is, ha az adatok gyakoriságok, a megfigyelési egység mindig az, amiben a gyakoriságot számoljuk – ehhez tartoznak ugyanis a megfigyelt számadatok – még akkor is, ha biológiailag az az érdekesebb, amit számolunk.
Természetesen az a legmegbízhatóbb vizsgálat, amikor a teljes populációt megvizsgáljuk, de ez gyakran lehetetlen vagy túlságosan költséges volna. Nyilvánvalóan lehetetlen végtelen populáció esetén, és akkor is, ha a vizsgálat során a vizsgált objektum megsemmisül vagy tönkremegy. Így a vizsgálat általában nem terjedhet ki a teljes populációra, csak egy kis részére, a mintára. A minta mérete (= mintanagyság, mintaelemszám) (sample size) mindig akkora kell, hogy legyen, amekkorára feltétlenül szükség van a megkívánt pontosságú vagy megbízhatóságú eredményekhez! Ha a minta túl nagy, az pazarlás (pénz, idő, energia), sőt ha a kísérleti alanyok emberek vagy állatok, akkor etikai problémákat is felvet a szükségtelenül kockázatnak vagy szenvedésnek kitett kísérleti alanyok miatt. Ha a minta túl kicsi, az pedig még nagyobb pazarlás, hiszen ha a kitűzött célt nem érjük el, akkor az összes ráfordítás kárba ment, és az összes kísérleti alanyt feleslegesen tettük ki kockázatnak vagy szenvedésnek. Ezért van szükség – olykor bonyolult – módszerekre az egyes vizsgálatokhoz szükséges mintaelemszám meghatározásához (lásd ??. és ??. fejezeteket).
A vizsgálatban a minta képviseli a populációt, fontos tehát, hogy jól tükrözze annak – a vizsgálat szempontjából lényeges – tulajdonságait. A mintát valamely szempontból reprezentatívnak nevezzük, ha abból a szempontból jól tükrözi a populációt. Lehet, hogy egy minta nem szerint reprezentatív, de életkor szerint nem. Valamely korcsoport lehet túlreprezentált, másik pedig alul reprezentált a mintában. Ez azt jelenti, hogy részaránya a mintában nagyobb, illetve kisebb, mint a populációban. Ne kergessünk délibábot, nincs olyan mintavételi módszer, amely minden szempontból tökéletesen reprezentatív mintát szolgáltatna! Ha lenne ilyen, a statisztika jókora része fölöslegessé válna.
Valószínűségszámítás és matematikai statisztika tankönyvekben gyakran olvassuk, hogy ,,legyen \(x_1, x_2, \ldots, x_n\) egy \(n\) elemű minta az \(X\) valószínűségi változóból’‘. Itt a minta szó nem a megfigyelési egységekre utal, hanem a rajtuk mért értékekre. A matematikai statisztikában populáció, illetve minta alatt nem megfigyelési egységeket, hanem az azokon mért számértékeket értik. Matematikai szempontból mindegy ugyanis, hogy a megfigyelési egységek állatok, növények vagy bármi más. Az is mindegy, hogy a mért adat az életkoruk, magasságuk vagy valami egyéb. Absztrakt matematikai értelemben a megfigyelési egységek azonosíthatók a rajtuk mért értékekből álló vektorokkal (= számsorokkal), így a minta is csak számokból áll. Egyes megfigyeléseket valóban nem lehet másként értelmezni: ha például minden reggel pontban kilenc órakor megmérem a szobámban a hőmérsékletet, akkor itt tényleg nincs egy ,,jobb’’ populáció, mint a lehetséges értékeké.
A statisztikai számítások kissé eltérnek véges és végtelen populációra, sőt véges populáció esetén az sem mindegy, hogy a mintavétel visszatevéssel vagy visszatevés nélkül történik. Visszatevéses mintavételnél ugyanaz a megfigyelési egység többször is beválasztható a mintába, míg visszatevés nélkülinél a már egyszer bekerültek nem választhatók még egyszer. Végtelen populációra a visszatevéses és visszatevés nélküli mintavétel közötti különbség elenyészik, ugyanis ekkor visszatevéses mintavétel esetén is 0 annak a valószínűsége, hogy egy megfigyelési egységet többször kiválasztunk. Ha a populáció véges ugyan, de nagyon nagy, akkor jó közelítéssel alkalmazhatjuk a végtelen populációt, illetve visszatevéses mintavételt feltételező módszereket. Pontosabban ez akkor igaz, ha a minta kicsi a populációhoz képest – mondjuk, ha egy több százezres populációból veszünk egy néhány százas, vagy egy többszázas populációból egy 10–20 elemű mintát.
Bár a leggyakrabban használt statisztikai eljárások végtelen populációt, illetve visszatevéses mintavételt feltételeznek, használatuk véges populáció és visszatevés nélküli mintavétel esetén is megengedett, ha a minta kisebb, mint a populáció 5%-a.
Jegyezzük meg tehát, hogy a matematikai statisztikában az alapértelmezés ,,a lehetséges értékek végtelen populációja’’ vagy ,,a lehetséges értékek véges populációja visszatevéses mintavétellel’’. Itt a hétköznapi ésszel sokkal természetesebb véges populáció és visszatevés nélküli mintavétel számít különlegesnek. Ennek ellenére, mivel ritka az olyan vizsgálat, amelyben a minta meghaladja a populáció 5%-át, ez alig okoz gondot.
2.2 Leíró és induktív statisztika
A leíró statisztika (descriptive statistics) a statisztikának az az ága, amelyik az adatokban rejlő információ emészthető formában való tálalásával foglalkozik. Ez jelentheti az adatok rendezését, csoportosítását (táblázatok), megjelenítését (grafikonok, diagramok, piktogramok), illetve statisztikai mérőszámokkal való jellemzését (minimum, maximum, átlag, szórás stb). A leíró statisztika azért fontos, mert nagy adatmennyiségek – több ezer adat – esetén hiába tennénk közzé az összes számot, közönséges halandó úgysem tudna mit kezdeni vele.
A leíró statisztika eszközei a különféle táblázatok (table), diagramok (chart, plot, diagram) és statisztikai mérőszámok (statistic). Az első kettőre példa az 2.1 táblázat és a 2.1. ábra, a statisztikai mérőszámokat pedig egyszerűen a szövegben szokás közölni, például így: ,,A mintában a testmagasság és a testtömeg között szoros összefüggést találtunk (Pearson-féle korrelációs együttható: \(r=0.53\))’’. Az ábrák információgazdagságának szép példája a népességtudományban használatos „korfa”, amely nem és kor szerinti bontásban szemlélteti a populáció összetételét (2.2. ábra).
| Testmagasság | <80 kg | ≥ 80 kg |
|---|---|---|
| <175 cm | 243 | 75 |
| ≥ 175 cm | 267 | 415 |
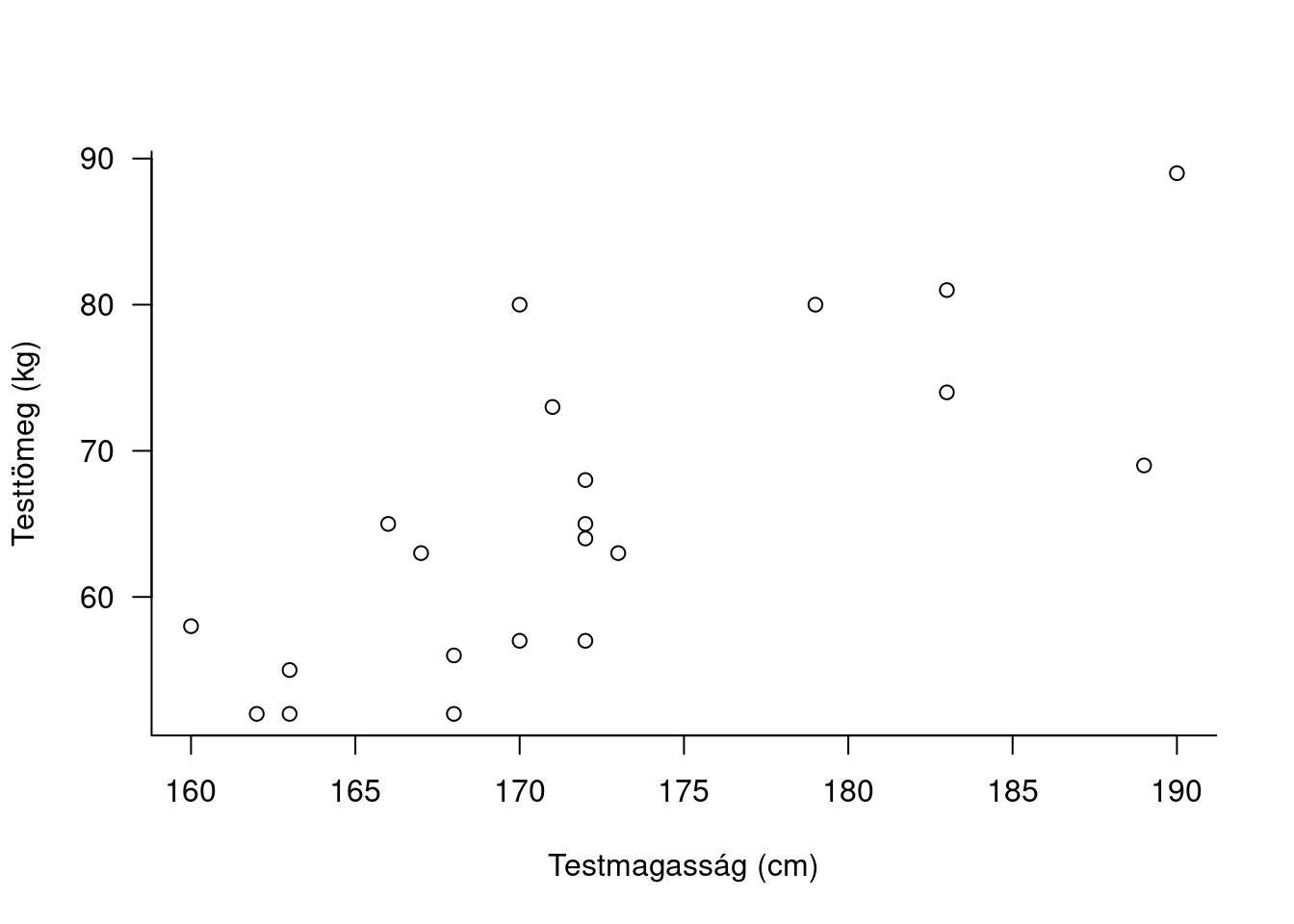
2.1: ábra. Testmagasság és testtömeg összefüggésének ábrázolása szórásdiagramma

2.2: ábra. A Föld lakosságának korfája 2006-ban (Forrás: U.S. Census Bureau, Inter-national Data Base)
Tipikus a leíró statisztika használata akkor, amikor teljeskörű adatfelvétel történik, például népszámlálási vagy választási adatok, bejelentési kötelezettséggel járó fertőző betegségek esetén, vagy ha egy vizsgált állattartó telepen valamennyi állat adatai rendelkezésre állnak stb. Már említettük azonban, hogy legtöbbször nincs módunk a teljes populációt megvizsgálni, ezért kénytelenek vagyunk csupán egy minta vizsgálatából levonni a populációra érvényes következtetéseket. Ekkor lép színre az induktív statisztika (statistical inference) az induktív szónak az ,,általánosító’’ értelmében (mint az egyediből az általánosra való következtetés). Természetes, hogy egy ilyen következtetéstől nem várjuk el, hogy 100% biztonsággal helyes legyen, csak azt, hogy ,,nagy valószínűséggel’‘, ami általában – szakterülettől függően – 90, 95 vagy 99%-os megbízhatóságot, azaz 10, 5 vagy 1% tévedési valószínűséget jelent. A megbízhatóság, illetve a tévedési valószínűség pontos jelentését nem könnyű megérteni. A legegyszerűbb, ha úgy gondolunk rá, hogy ,,ha sokszor alkalmazzuk a szóban forgó módszert, akkor várhatóan az esetek hány százalékában kapunk helyes, illetve téves eredményt’’.
Az induktív statisztika két legjellemzőbb feladata a becslés (estimation) és a hipotézisvizsgálat (hypothesis testing). A becslés a ,,Mennyi? Mekkora? Hány százalék? stb.’’ kérdésekre vár választ, mégpedig egy (vagy néhány) számot. A hipotézisvizsgálatban ezzel szemben ,,Igen/Nem’’ választ várunk az ,,Igaz-e? Fennáll-e? Van-e összefüggés …? Van-e hatása …? Van-e különbség …? stb.’’ kérdésekre.
A leíró és induktív statisztika nem mindig választható szét élesen. Amikor több ezres mintákkal dolgozunk, akkor már a minta jellemzéséhez is szükség van a leíró statisztika módszereire, bár a fő cél ilyenkor is a populációra érvényes következtetések levonása, amelyhez az induktív statisztika szükséges. Másfelől kis minták esetén is előnyös a leíró statisztika módszereinek – különösen a grafikus megjelenítésnek – az alkalmazása azért, hogy az információkat szemléletesebben, illetve hatásosabban tudjuk közölni. Az induktív statisztikai vizsgálatokban azért is fontosak a leíró statisztika módszerei, mert segítségükkel jobban átláthatjuk adatainkat, észrevehetjük olyan tulajdonságaikat, amelyek döntően befolyásolják az elemzésükhöz legmegfelelőbb módszerek kiválasztását.
2.3 Mintavételi módszerek
Az induktív statisztikában a mintából vonunk le a populációra érvényes következtetéseket. Nem mindegy azonban, hogy miként választjuk ki a mintát a populációból. A mintavétel módjától függ többek között az is, hogy az elemzésre milyen eljárásokat, illetve az eljárásoknak milyen változatait kell vagy lehet használnunk. A bevezető statisztika kurzusokon ismertetett módszerek és számítások általában a legegyszerűbb esetre, az egyszerű véletlen mintavételre érvényesek. Egyszerű véletlen mintavétel (simple random sampling) esetén az alapsokaság minden egyede egyforma eséllyel kerül a mintába. A mintavétel lehet visszatevéses (sampling with replacement) vagy visszatevés nélküli (sampling without replacement) (vö. 2.1. fejezet). Véges populáció esetén a visszatevés nélküli mintavétel a természetesebb, ha kivitelezhető. (Nem kivitelezhető, ha a megfigyelési egységek azonosítása nem megoldható, például utasok, vásárlók, éttermi vendégek számlálásakor, vadon élő állatok kamerás megfigyelése esetén stb.)
Végtelen populáció vagy visszatevéses mintavétel esetén a mintabeli értékek mint valószínűségi változók függetlenek (independent) egymástól (vö. ??. fejezet), amit röviden a ,,mintaelemek függetlensége’’ vagy a ,,független minta’’ elnevezésekkel fejezhetünk ki. Ez a legtöbb klasszikus statisztikai eljárás alkalmazhatóságának egyik feltétele. Véges populáció és visszatevés nélküli mintavétel esetén ez nem teljesül, de közmegegyezés szerint nagy populációból vett viszonylag kis minta esetén mégis megengedett e módszerek használata (vö. 2.1. fejezet). (Megjegyezzük, hogy ma már olyan módszerek is vannak, amelyeknek nem feltétele a mintaelemek függetlensége (Pinheiro and Bates (2006), Faraway (2016)).)
Ha az alapsokaságot valamilyen szempont (nem, kor stb.) szerint részekre bontjuk, és ezekből az ún. rétegekből egymástól függetlenül veszünk egyszerű véletlen mintákat, akkor rétegzett mintavételről (stratified sampling) beszélünk. Ha az egyes rétegekből vett minták nagysága arányos a rétegek populációbeli részarányával, akkor a rétegzett minta majdnem ugyanolyan, mint egy, a populációból vett egyszerű véletlen minta (de azért nem teljesen, mert az egyszerű véletlen mintában az egyes rétegek részaránya a véletlentől függ, míg a rétegzettben előre be van állítva). De a rétegzett mintavétel általában nem így történik, legtöbbször minden rétegből ugyanakkora mintát veszünk (például 100 nő és 100 férfi vagy 300 beteg és 300 egészséges stb.), mert közel azonos méretű mintákkal a statisztikai elemzések általában hatékonyabbak.
Mind az egyszerű véletlen, mind a rétegzett mintavétel általában a populációról készített teljes lista és sorsolás segítségével történik. A sorsoláshoz régebben kizárólag véletlenszám-táblázatokat használtak, de ma már gyakran számítógéppel (véletlenszám-generátorral) végzik.
Ha R-ben szeretnénk mondjuk az \(1\dots1000\) számok közül véletlenszerűen kiválasztani 20-at, akkor azt a következő kóddal tehetjük meg:
(minta = sample(1000, 20))## [1] 742 384 143 560 875 427 453 811 76 230 572 488 693 371 460 889 233 894 88
## [20] 772Az így kapott véletlen sorszámokat a sort() függvénnyel rendezhetjük nagyság szerint:
sort(minta)## [1] 76 88 143 230 233 371 384 427 453 460 488 560 572 693 742 772 811 875 889
## [20] 894Gyakran lehet hallani vagy olvasni, hogy a véletlen mintavételnek az a legnagyobb előnye, hogy a populációt a lehető legjobban reprezentáló mintát szolgáltat. Ez nem egészen így van: ha a mintavételt a véletlenre bízzuk, akkor ezzel éppen hogy megengedjük, hogy a minta esetleg ne legyen reprezentatív. Például, egyáltalán nem meglepő, ha egy egyszerű véletlen minta kormegoszlása eltér a populációétól. Ha azt szeretnénk, hogy a mintabeli kormegoszlás pontosan megegyezzen a populációbelivel, akkor kor szerint rétegzett mintát kell vennünk, minden korosztályból akkora mintát véve, amely arányos a korosztály populációbeli részarányával. Az egyszerű véletlen mintavétel nagy valószínűséggel ennél – legalábbis ebből a szempontból – rosszabb mintát produkál. Tehát, ha valamilyen szempontból fontos a reprezentativitás, akkor aszerint a szempont szerint érdemes rétegeznünk.
Akkor vajon mi az az előnye a véletlen mintavételnek, amely ilyen népszerűvé teszi? Az, hogy a minták különbözőségéből, változékonyságából adódó bizonytalanság, illetve ingadozás matematikai eszközökkel kiszámítható abból a feltételből kiindulva, hogy az összes lehetséges minta egyformán valószínű. Tehát bármely, a mintából számított érték (minimum, maximum, átlag stb.) – a minta véletlenségéből következően – egy olyan véletlen szám (valószínűségi változó) lesz, amelynek eloszlása a valószínűségszámítás segítségével kiszámítható.
Sajnos véletlen mintavételre nem mindig van módunk. A legfőbb akadály általában az, hogy nincs – és gyakran nem is készíthető – teljes felsorolás a populációbeli megfigyelési egységekről. Végtelen populáció esetén ez nyilvánvalóan lehetetlen, de gyakorlatilag véges populáció esetén is sokszor kivihetetlen. Az is előfordulhat, hogy lista ugyan készíthető – például a TAJ-szám segítségével – de ezen a listán keresztül az egyedek nem elérhetőek (például mert a lista a lakcímüket nem tartalmazza). Ilyen esetekben más mintavételi módszerekre kényszerülünk.
Szabályos, szisztematikus mintavétel (systematic sampling) esetén csak az első egyedet választjuk véletlenszerűen, a többit meghatározott mintavételi intervallumok kihagyásával (például minden tizedik egyedet választjuk be vagy háromnaponként mintavételezünk). Ezt a módszert leggyakrabban akkor szokták használni, ha az egyedek spontán jelennek meg a vizsgálat látókörében, például betegek a rendelőben, ügyfelek a hivatalban, vásárlók a boltban, jegypénztárnál, állatok az itatónál stb. Szisztematikus mintavétel esetén a szokásos – a valószínűségszámítás alkalmazásával nyert, véletlen mintákra érvényes – statisztikai következtetéseket (konfidencia-intervallumok, \(p\)-értékek stb.) fenntartással kell kezelnünk. Az a gond ugyanis, hogy a mintavételi szabályunk összefügghet valamely más változóval, és ekkor könnyen lehet, hogy a minta már nem reprezentálja jól a populációt: ez az úgynevezett mintavételi torzítás (sampling bias). Például, ha a rendelőben vagy a hivatalban minden nap az első beteget vagy ügyfelet választjuk a mintába, akkor a koránkelők vagy a munkába sietők túl lesznek reprezentálva a ráérősökhöz képest (vagy az aktív dolgozók a nyugdíjasokhoz képest). Ha sorsolással választunk, akkor ilyen torzítás szóba sem jöhet, hiszen a véletlen számok a vizsgált folyamat változóival semmiképpen nem függhetnek össze.
Csoportos (klaszteres) mintavételről (cluster sampling) akkor beszélünk, ha a megfigyelési egységeket nem tudjuk egyenként, egymástól függetlenül kiválasztani (egy alom, egy fészekalj madárfióka, egy gazdapéldányon fellelt paraziták, egy háztartásban élő emberek, egy iskolai osztály stb.). Általában ezt a mintavételi módszert sem saját jószántunkból választjuk, hanem a körülmények kényszerítenek rá. A klasszikus statisztikai eljárások alkalmazása ilyenkor nem helyénvaló, mert azok független mintát kívánnak, de ma már szép számmal vannak kifejezetten ilyen adatok elemzésére való módszerek is (Pinheiro and Bates (2006), Faraway (2016)). Azt azért általában ezek is feltételezik, hogy a csoportok kiválasztása (a csoportok populációjából!) véletlen mintavétellel történt.
Természetesen a felsoroltakon kívül még nagyon sok más mintavételi módszer létezik. Könyvünkben a módszereknek és mutatóknak csak az egyszerű véletlen mintavétel esetére érvényes változatát ismertetjük. Ha más mintavételi eljárással dolgozunk, akkor elképzelhető, hogy már olyan egyszerű mutatókat is, mint az átlag vagy a szórás, más képlettel kell számolni. Ha a Kedves Olvasó további mintavételi eljárásokat szeretne megismerni, vagy arra kíváncsi, hogy az egyes mintavételi módszerek esetén hogyan módosulnak az elemzések és számítások, akkor figyelmébe ajánljuk Cochran klasszikus munkáját (Cochran (1977)).
2.4 Adatok
Egy kutatási kérdés felvetődésétől általában több lépésen – és nagyon sok fáradságon – keresztül vezet el az út addig, amíg a vizsgálat adatai összeállnak. Ilyen lépések a kutatási kérdés pontosítása, operacionalizálása (= mérhető formában való megfogalmazása), a megválaszolásához szükséges mérési módszerek megválasztása vagy kidolgozása, a vizsgálat részleteinek megtervezése, a megfigyelési egységek kiválasztása, esetleges előkísérletek stb. Ezekkel a kérdésekkel most nem kívánunk foglalkozni, csak annyit jegyzünk meg, hogy ezek mind a kísérlettervezés (experimental design, study design) vagy a kutatásmódszertan, illetve kutatástervezés (research methodology, research planning) témakörébe tartoznak.
A vizsgálat elvégzése után az összegyűlt adatokat hagyományosan papíron tárolták, manapság pedig a számítógépen, általában valamilyen táblázatkezelő program segítségével (Excel, Calc stb.). Mivel a táblázatkezelő programok a kockás papírt utánozzák, az emberek a számítógépes tárolásra is ugyanolyan formát szoktak választani, mintha papírra írnának, azaz amely a legkevesebb írásmunkával jár, és a szemnek is a legáttekinthetőbb. Általában több kisebb, jól áttekinthető táblázatba csoportosítják az adatokat, kerülik az ismétlést, ismétlődő adatokat inkább fejlécbe tesznek, fontos adatokat színekkel, kiemelésekkel, magyarázó szövegekkel jeleznek.
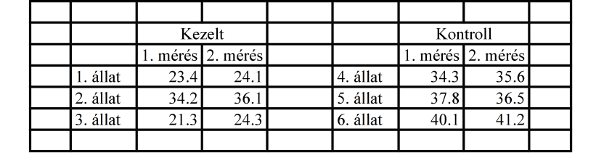
Sajnos a statisztikai programok másképp – sokkal egyszerűbben, mondhatni egészen bután – gondolkodnak, számukra az egyetlen érthető forma a legegyszerűbb, csoportosítás és kiemelések nélküli elrendezés, egyetlen fejléccel, egyes adatokat akár ezerszer is megismételve: ez az úgynevezett adatmátrix.
2.4.1 Adatmátrix
Az adatmátrix (data matrix) – az R-ben ,,data frame" a neve – egy olyan táblázat, amelynek minden sora egy megfigyelési egységnek (személy, állat, vérminta stb.), oszlopai pedig az egyes mért vagy megfigyelt adatoknak (kor, nem, testtömeg stb.) felelnek meg. A sorokat eseteknek (case), az oszlopokat változóknak (variable) nevezzük. Ezt a szokásos elrendezést és elnevezéseket azért kell ismernünk, mert a statisztikai programok legtöbbje – így az R is – az elemzendő adatokat ilyen formában várja, az eredmények kiírásakor pedig rendszerint a ,,case" és ,,variable" elnevezéseket használja. A továbbiakban a ,,megfigyelési egység" helyett mi is legtöbbször a rövidebb ,,eset" elnevezést fogjuk használni, a ,,megfigyelési egységeken mért adat" helyett pedig ,,változó"-t mondunk. Célszerű az adatmátrixot úgy elkészíteni, hogy első sora a változók nevét tartalmazza, mert az R ezeket a neveket át tudja venni, és később a változókra az R-ben is ezekkel a nevekkel hivatkozhatunk. Arra is van mód, hogy az adatmátrix valamelyik oszlopa az esetek nevét vagy azonosítóját tartalmazza. Adatok adatmátrix formában való elrendezésére példát mutat az alábbi táblázat.
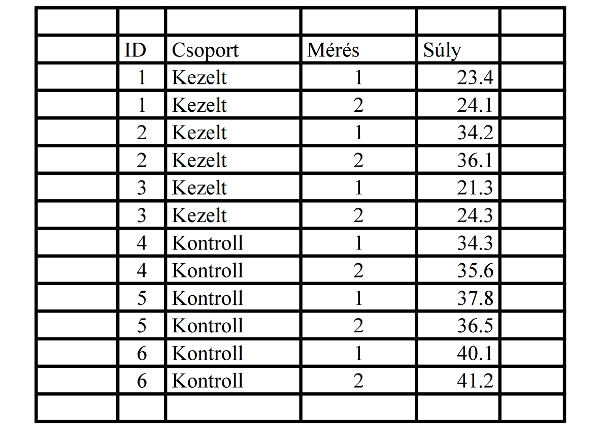
Az adatok lehetnek akár számértékek, akár szöveges adatok, akár kódok. A kódok olyan értékek, amelyek csak azonosításra szolgálnak: legyenek bár számok, akkor sem számolhatunk velük: ilyen például a táblázatban az ID nevű változó.
Ha az adatbevitelt táblázatkezelő programmal végeztük, és az adatokat már a fenti – az adatmátrixnak megfelelő – formában rendeztük el, akkor csak az a kérdés, hogy hogyan tudjuk ezt az R-nek átadni.
Erre egy egyszerű és kényelmes módszer a táblázat ,,csv" (= comma separated values) formában való mentése, majd az R read.table() függvényével való beolvasása.
2.4.2 Adattípusok, mérési skálák
Láttuk, hogy az adatmátrixban nemcsak számok szerepelhetnek, hanem szöveges adatok, dátumok és kódok is. A változók típusa meghatározza, hogy milyen műveleteket végezhetünk velük. Említettük azt is, hogy a számokkal nem mindig számolhatunk, például fülszám, helyrajzi szám stb. (Persze, aki statisztika címén csak átlagot tud számolni, az mindenből átlagot számol. Anekdoták szólnak arról, hogy botcsinálta ,,statisztikusok" olykor még a betegségkódokból és a postai irányítószámokból is átlagot számoltak.)
Az adatokat sokféleképpen lehet típusokba sorolni, a különböző statisztika könyvekben többféle rendszerrel is találkozhatunk, amelyek közül csak kettőt ismertetünk részletesen. Az egyik a változók mérési skála (measurement scale) szerinti csoportosítása. Ebben négy mérési skálát különböztetünk meg: nominális, ordinális, intervallum- és abszolút (vagy arány-) skálát. A másik csoportosítás két típust tartalmaz: kvalitatív és kvantitatív változókat. A kvalitatív változók nagyjából lefedik a mérési skála szerinti csoportosításban az első két, a kvantitatívak pedig a második két típust.
A nominális (nominal) változó – mint a neve is mutatja – csak megnevez, kategorizál, csoportba sorol, kódol. Értékei lehetnek akár szövegek, nevek, akár számok, számolni nem lehet velük, se összeadni, se szorozni, sőt az értékeknek még a nagyság szerinti sorrendje sem bír semmilyen jelentéssel. Nominális változók a szemszín, családi állapot, felekezeti hovatartozás, településnév vagy -kód, helyrajzi szám, postai irányítószám, személyi szám, TAJ-szám, betegségkód, talajtípus stb. Magyarul a nominális változót nevezik csoportosító, csoportképző, megállapítható, kategóriás vagy kategoriális változónak is.
Nominális változókkal nem nagyon lehet mást csinálni, mint leszámlálni, hogy az egyes kategóriákba hány eset, illetve az esetek hányadrésze, vagy hány százaléka esik. Az ilyen adatokat gyakorisági adatoknak (frequency data) nevezzük.
Az ordinális (ordinal) változó szintén csoportba sorol, de értékeinek egyértelmű természetes sorrendje van. Ugyan számolni a kódokkal most sem tudunk (a kódok lehetnek akár betűk is), de rendezettek, azaz sorrendjük értelmes jelentéssel bír. Ilyen változó például a vizsgaeredmény, amelyet egyes országokban betűkkel, más országokban számokkal kódolnak. Az persze vicces, hogy attól, hogy az osztályzatok számok, mindjárt ellenállhatatlan vágyat érzünk, hogy tanulmányi átlagot számoljunk. (Ahol a vizsgaeredményeket A, B, C-vel kódolják, nincs ilyen kísértés.) Ugyancsak ilyen változó az iskolai végzettség, akár kódszámokkal jelöljük, akár nevekkel. Sok kódolt változó is ordinális, például az alkoholfogyasztást kódolhatjuk így: 1 = soha, 2 = évente egyszer-kétszer, 3 = havonta egyszer, 4 = hetenként, 5 = hetenként többször, 6 = minden nap. Nyilvánvaló, hogy a számok itt sem szám-mivoltukban jelennek meg.
Az ordinális változóknál is a gyakoriságok leszámlálása az egyetlen értelmes összesítés, de itt már – a természetes rendezés miatt – a kumulatív gyakoriságok is értelmesek. A kumulatív (halmozott) gyakoriság (cumulative frequency) azt jelenti, hogy nemcsak az adott osztályba eső egyedeket számoljuk össze, hanem az adott és az összes őt megelőző osztályba tartozókat is (lásd még a ??. fejezetben is).
Elsőéves férfi biológus hallgatók – egy (elképzelt) 1000 fős populáció, amely a későbbiekben több példában is előkerül – matematika osztályzatairól készítünk gyakorisági táblázatot a table() függvénnyel.
Az adatokat a pop nevű adatmátrix – R-es szóhasználattal data.frame – tartalmazza.
Az adattáblázat matek nevű oszlopára pop$matek néven hivatkozhatunk.
A gyakorisági táblázat:
table(pop$matek)##
## 1 2 3 4 5
## 232 198 188 191 191A kumulatív gyakoriságokat (jelentésük: hányan kaptak legfeljebb kettest, legfeljebb hármast stb.) az előbbi táblázatból a cumsum() függvénnyel készíthetjük el:
cumsum(table(pop$matek))## 1 2 3 4 5
## 232 430 618 809 1000Az intervallumskálán (interval) mért változóval már végezhetünk összeadást és kivonást, de a 0 érték nem az abszolút nulla, ezért a szorzás-osztás és az arányítás (,,kétszer akkora“, ,,harmadannyi”) nem értelmes. A valódi számszerű változóink többnyire ilyenek, ezekkel már gyakorlatilag mindegyik statisztikai módszer működik. Nyilvánvalóan ilyen a Celsius- vagy a Fahrenheit-skálán mért hőmérséklet, ahol a 0 , illetve a 0 önkényesen választott 0 pontok (ellentétben a Kelvin-skálával, amelynél a 0 abszolút nullának tekinthető). Valójában az abszolút nullában az ember csak nagyon ritkán lehet biztos – még az életkort is számíthatjuk a születés helyett a fogamzástól.
Az arány- vagy abszolút (ratio, absolute) skálán mért változóknak a 0 abszolút nulla pontja, ezért ezekkel már a szorzás és osztás is megengedett, mondhatjuk, hogy ,,\(x\) kétszer akkora, mint \(y\)" stb.
Sok fizikai változó ilyen, mint például a hosszúság vagy a tömeg, a darabszámok stb.
Szintén abszolút skála a hőmérséklet mérésére a Kelvin-skála.
Ritka az olyan statisztikai eljárás, amelyik csak arányskálájú adatokra alkalmazható – ilyen például a relatív szórás (lásd ??. fejezet) vagy az origón átmenő regresszió (lásd ??. fejezet) – a legtöbb módszer megelégszik intervallumskálájú adatokkal.
Fontos észben tartani, hogy egy változóhoz nem eleve adott, hogy milyen skálájú, hanem mindig mi döntjük el, hogy milyen skálájúnak ésszerű tekintenünk. Sőt, már azt is mi döntjük el, hogy egyáltalán hogyan mérjünk egy bizonyos, minket érdeklő mennyiséget. Például, ha egy anyag jelenléte érdekel a vérben, akkor mérhetjük egy gyors teszttel, amely csak igen-nem választ ad, és amelyet esetleg kiegészíthetünk egy ,,lehet, de nem egyértelmű" kategóriával a határesetekre: így egy ordinális skálájú változóhoz jutunk. Ha műszeres mérést végzünk, akkor egy számértéket kapunk az anyag koncentrációjára. Ha úgy akarjuk, tekinthetjük ezt a változót abszolút skálájúnak, de elképzelhető, hogy a nulla pont a műszer kalibrálásától függ, ezért lehet, hogy jobb, ha csak intervallumskálájúnak tekintjük.
Vagy képzeljük el, hogy zajszintet mérünk egy olyan műszerrel, amelyen egy gombbal beállíthatjuk, hogy \(W/m^2\)-ben vagy \(dB\)-ben mérjen. A mért érték mindkét esetben egy fizikai mennyiség számszerű kifejezése, bármelyikre könnyen rámondanánk, hogy intervallum-, sőt akár hogy abszolút skálájú. De tudjuk, hogy a \(dB\) skála logaritmus-transzformáltja a másiknak, tehát nem lehet mindkettő még intervallumskálájú sem! Akkor melyik az igazi? Érvelhetünk úgy, hogy a \(W/m^2\) az a fizikai mennyiség, amelynek abszolút nulla pontja van, a teljes csend, a másik pedig származtatott változó, tehát az nem lesz sem abszolút, sem intervallumskálájú. De tudjuk, hogy hangosság-érzetünket a \(dB\) skála tükrözi hívebben: a zajt annyival érezzük erősebbnek, amennyivel az a \(dB\) skálán mérve nagyobb, tehát az érzékelt hangosságbeli különbségeket az tükrözi hívebben. Az, hogy melyiket tekintsük intervallumskálájúnak, attól függ, hogy a fizikai inger, vagy az érzékelés szintjén szeretnénk-e kifejezni a zaj erősségét. Azt pedig, hogy kutatási céljainknak melyik a megfelelőbb, mindig magunknak kell eldöntenünk.
Külön említést érdemelnek azok a nominális változók, amelyeknek csak két értékük van. Ezek az úgynevezett dichotom vagy bináris (dichotomous, binary) változók. Ezekre egészen speciális elemzési módszereket dolgoztak ki. A dichotom változók két értéke gyakran természetes módon rendezett, például amikor a két lehetséges érték igen/nem, van/nincs, pozitív/negatív stb. Ilyenkor bizonyos elemzésekben tekinthetjük őket ordinális skálájúnak is, így például beszélhetünk két tulajdonság megléte között vagy két diagnosztikai teszt eredménye között fennálló pozitív vagy negatív korrelációról.
A másik csoportosítás szerint a nominális és ordinális változókat együtt kvalitatív változóknak, vagy R-es szóhasználattal faktoroknak (factor) nevezzük. Ezeket kódolhatjuk szöveggel, betűkóddal, vagy akár számmal is, de matematikai műveleteket akkor sem végezhetünk velük. Ha az R-ben faktorral próbálunk matematikai műveletet végezni, figyelmeztető üzenetet kapunk.
A kvantitatív változók – az R-ben numerikus (numeric) változóknak nevezik őket – magukban foglalják az intervallum- és az abszolút skálájú változókat. Ezekkel az R az összes matematikai számítást megengedi. Később látunk majd rá példát, hogy az R valamely eljárást faktorokkal és numerikus változókkal egyaránt végrehajt, de a számítások – és persze az eredmények is – különböznek aszerint, hogy az elemzést faktorral vagy numerikus változóval végezzük.
Ha egy változó értékei nem számok, akkor azt a változót az R magától is faktornak tekinti.
De ha egy faktort számokkal kódolunk, akkor az R-nek külön meg kell mondanunk, hogy ez faktor (különben az R azt feltételezi, hogy a számok tényleg számok, ami az elemzések eredményére is hatással van).
Erre szolgálnak a factor(), illetve a as.factor() függvények. Ha a matek
változót faktorrá szeretnénk alakítani:
pop$matek = factor(pop$matek)
str(pop$matek)## Factor w/ 5 levels "1","2","3","4",..: 3 1 5 1 1 4 3 2 5 4 ...A faktorrá alakítás után ellenőrzésképpen az str() függvényt is meghívtuk.
A függvény felsorolja a faktor kategóriáinak nevét (a példában az idézőjel jelzi, hogy ezek nevek és nem számok), majd az adatmátrix első néhány esetére a faktor belső kódjait.
A kvantitatív – azaz számértékű – változókat tovább bonthatjuk diszkrétekre és folytonosakra. Diszkrét változónak (discrete variable) az olyan változót nevezzük, amelynek összes lehetséges értékét szépen egymás után fel tudjuk sorolni úgy, hogy van egy első érték, egy második érték stb. Ezt nyilvánvalóan mindig megtehetjük, ha a lehetséges értékek halmaza véges, és esetenként akkor is, ha végtelen (például, ha az értékek a természetes számok).
Folytonos változónak (continuous variable) az olyan változót nevezzük, amelynek lehetséges értékei a számegyenesen egy folytonos tartományt – például egy intervallumot – alkotnak. Az intervallum lehet végtelen hosszú is, sőt akár a teljes számegyenes is (= az összes valós szám).
A változók szokásos csoportosításait a 2.3. ábra foglalja össze.

2.3: ábra. Változók osztályozása
A kvantitatív változók – legyenek akár diszkrétek, akár folytonosak – matematikai modellje a valószínűségszámításban a valószínűségi változó. Erről részletesebben ??. fejezetben lesz szó.
2.4.3 Transzformációk, származtatott változók
Mivel az alábbiakban több olyan dologról is említést teszünk, amelyek kezdők számára valószínűleg nem sokat mondanak, azt ajánljuk, hogy a statisztikával most első ízben ismerkedők ezt a fejezetet a becslések és hipotézisvizsgálatok ismeretében olvassák majd újra.
Származtatott vagy képzett változónak az olyan változót nevezzük, amelyet nem megfigyelünk, hanem más változókból matematikai vagy logikai műveletekkel számolunk ki. Ilyenek például a testtömeg-index, a ,,fehérje % a szárazanyagban", vagy kérdőíves felméréseknél egy kérdéscsoportra adott pontszámok összege stb. Ilyen származtatott változókat nagyon könnyen készíthetünk az R-rel, nem érdemes erre másik programot használni.
Számítsuk ki az elsőéves egyetemisták testtömeg-indexét (body mass index, BMI) a magasságuk (magas) és testtömegük alapján (tomeg)!
A testtömeg-index képlete: \[ BMI = \frac{\text{testtömeg}}{\text{magasság}^2}, \] a testtömeget kg-ban, a magasságot méterben mérve. A megfelelő R kód:
pop$BMI = pop$tomeg/pop$magas^2 * 10000Az 10000-rel való szorzásra azért van szükség, mert a pop adattáblázatban a magasság cm-ben van megadva.
Az eredmény (csak a pop állomány első három sorát, azaz az első három eset adatait íratjuk ki):
pop[1:3, ]## magas tomeg matek biol matek.kat BMI
## 1 183 73 3 3 rossz 21.80
## 2 176 99 1 3 rossz 31.96
## 3 179 84 5 5 jo 26.22Gyakran az a helyzet, hogy nem tudjuk – vagy túl nehéz lenne, ezért nem éri meg – azt a változót megmérni, amire szükségünk lenne, de helyette meg tudunk mérni egy másikat, amelyikből amaz közelítőleg meghatározható. Ilyen eset például, amikor egy szerv vagy képlet térfogatát, illetve tömegét kell meghatároznunk ultrahangos vizsgálat alapján, vagy ha egy állat testfelszínét kell megbecsülnünk a lineáris méreteiből. Ilyenkor általában elméleti megfontolásokon alapuló – pontos vagy közelítő – képletekkel számolunk.
Néha a szakma hagyományai határozzák meg, mit hogyan szokás transzformálni. Van olyan szakterület, ahol inkább a hullámhosszal, máshol inkább a frekvenciával ,,illik" dolgozni. Szintén a tradíció dönti el, hogy a hidrogénion-koncentrációval vagy a pH-val számolunk-e.
De az is lehet, hogy ,,ad hoc" csak azért transzformálunk, hogy az adatokra teljesüljenek valamely statisztikai módszer alkalmazhatósági feltételei. Ilyenkor legtöbbször az a cél, hogy (1) a transzformált változó eloszlása közelítőleg normális legyen, vagy (2) regressziószámításnál a függő változó szórása a magyarázó változók teljes tartományában azonos legyen, vagy (3) két változó közötti nemlineáris kapcsolat lineárissá váljon. Most csak az elsővel foglalkozunk, a másik kettőről a regressziószámításról szóló, 9. fejezetben lesz szó. Vigyázzunk, megtörténhet, hogy egy bizonyos célra alkalmas transzformációnak más szempontból ,,káros mellékhatása" van, például egy, a linearizálás céljából alkalmazott transzformáció elronthatja a normalitást.
Egy változó eloszlásán (distribution) egyelőre értsük azt a mintázatot, ahogyan a megfigyelt pontok elhelyezkednek a számegyenesen a ábrán. (Az eloszlásokkal kapcsolatban lásd még a 3.4. és 3.5. fejezeteket.) Ebben az értelemben egy tartományon egyenletes (uniform) eloszlásról akkor beszélünk, ha a tartomány egyik részében sem sűrűbb a pontok mintázata, mint másutt (2.4. ábra (a) adatsor). Egycsúcsú (unimodal) eloszlásról akkor beszélünk, ha a megfigyelések a tartományban egy hely környékén sűrűbbek, mint másutt (2.4. ábra (b) adatsor), többcsúcsúról (multimodal) pedig akkor, ha több ilyen sűrűsödési hely van (2.4. (c) adatsor). A ,,csúcs" elnevezés magyarázatáról lásd a 4. ábrát 3.4. fejezetben. Ferde (skewed) eloszlás az olyan, amelyik egycsúcsú ugyan, de nem szimmetrikus: a sűrűsödési helytől balra és jobbra távolodva a pontok sűrűsége nem azonos mértékben csökken (2.4. ábra (d) és (e) adatsorok). Úgy is mondhatjuk, hogy a pontok egyik irányban jobban elnyúló mintázatot mutatnak. A nagyobb értékek irányában (jobbra, felfelé, \(+\) irányban) elnyúló eloszlást jobbra ferdének (right skewed) (2.4. ábra (d) adatsor), a kisebb értékek felé (balra, lefelé, \(-\) irányban) elnyúlót pedig balra ferdének (left skewed) nevezzük (2.4. ábra (e) adatsor).
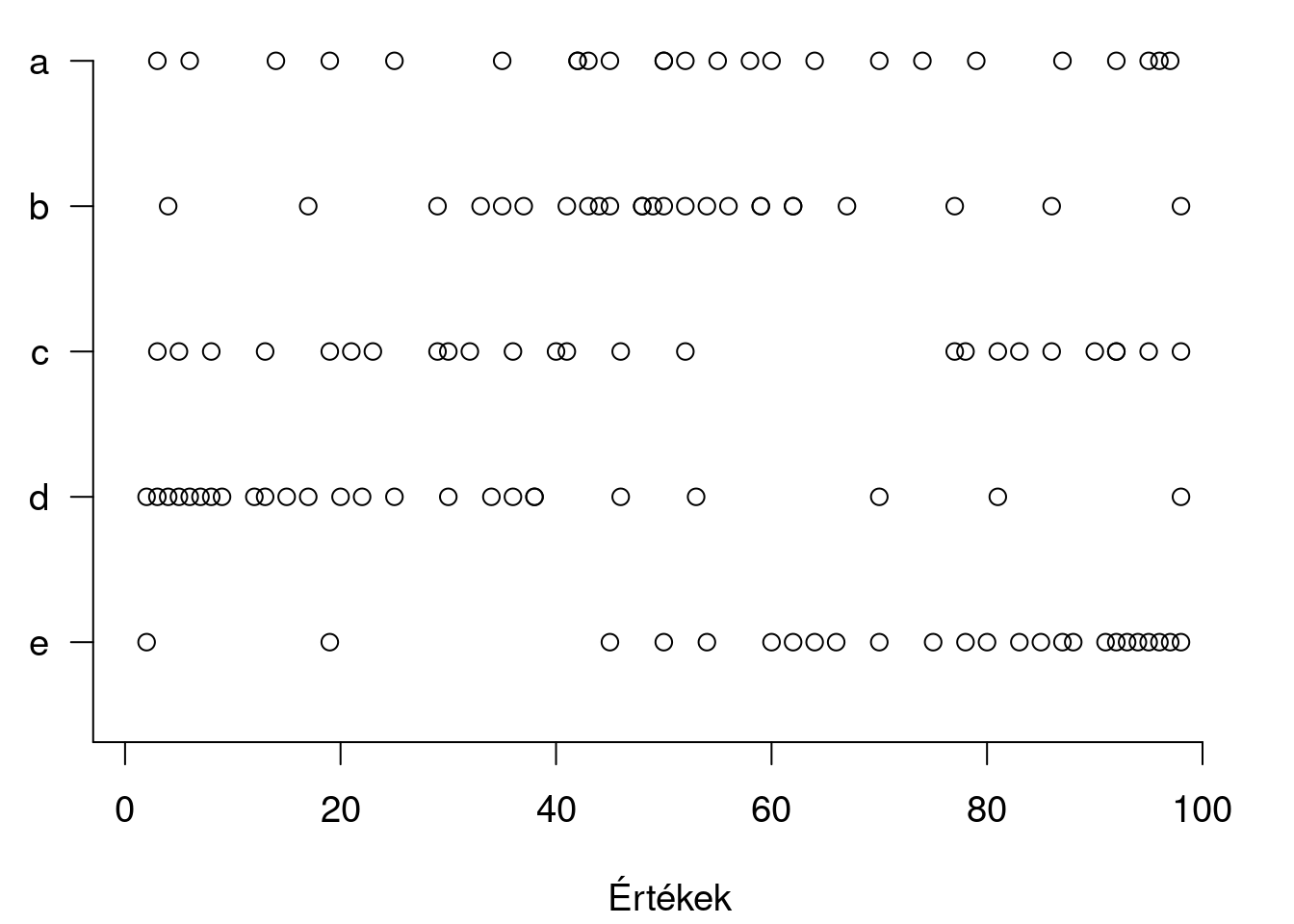
2.4: ábra. Különböző eloszlás-mintázatok
Jobbra ferde az összes olyan változó, amelyek értékei nem lehetnek negatív számok, de szélsőségesen nagy értékek azért előfordulnak. Tipikusan ilyen a jövedelem-eloszlás.
A normális vagy Gauss-eloszlás (normal distribution, Gaussian distribution) egycsúcsú, szimmetrikus eloszlás: a sűrűsödési hely a tartomány közepén van, és tőle balra és jobbra a pontok sűrűsége a távolságtól függően ugyanolyan ütemben csökken (2.4. ábra (b) adatsor). (A normális eloszlásnak ezen kívül még más, sajátos tulajdonságai is vannak, de azoknak már nincs olyan szemléletes jelentése, amely pusztán a mintázat szemrevételezése útján észlelhető.) A statisztikában a normális eloszlás azért játszik különösen fontos szerepet, mert a vizsgált változók nagyon gyakran – legalábbis közelítőleg – normális eloszlásúak, valamint mert sok statisztikai eljárás csak normális eloszlású változókkal működik helyesen. Azért, hogy ezeket az eljárásokat is alkalmazni lehessen, bevett szokás, hogy a ferde eloszlású változókat különféle transzformációkkal próbálják normális eloszlásúvá tenni (sajnos, elég gyakran gondolkodás nélkül). A leggyakoribbak a hatvány- és gyök-, valamint az exponenciális és logaritmus-transzformációk.
Jobbra ferde eloszlás esetén a gyök- vagy a logaritmus-transzformáció segíthet (2.5. ábra), balra ferde eloszlás esetén a hatvány- vagy exponenciális függvénnyel való transzformáció. Ezek mind úgy működnek, hogy megváltoztatják az értékek közötti távolságokat: az értéktartomány egyik szélén nyújtják, a másikon pedig összenyomják a skálát.
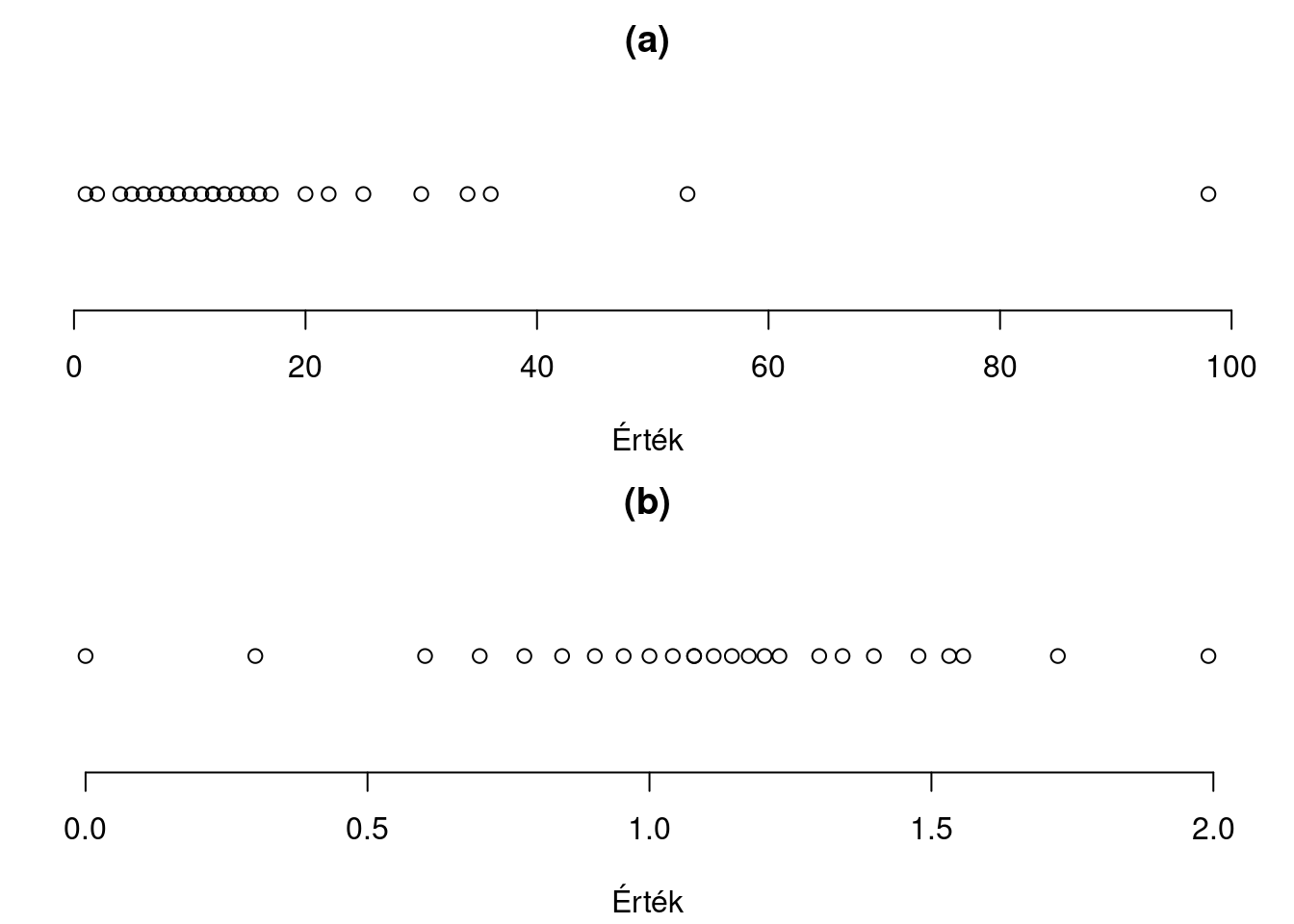
2.5: ábra. Jobbra ferde eloszlásból származó 25 érték (felső) és és logaritmus-transzformáltjaik (alsó)
Más esetekben másfajta transzformációkkal érdemes próbálkozni – relatív gyakoriságokra például az arcsin (arkusz szinusz) függvényt szokták ajánlani –, de a sikerre nincs garancia, előfordulhat, hogy az eloszlást semmilyen transzformációval nem tudjuk – még közelítőleg sem – normálissá tenni.
Két fontos figyelmeztetés!
Megtörténhet, hogy az eredeti adatok biológiailag jól interpretálhatók, a transzformált adatoknak viszont már nem tudunk biológiai jelentést tulajdonítani. Ilyenkor inkább ne transzformáljunk, hanem keressünk ferde eloszlásokkal is működő módszereket!
Ne akarjuk mindenáron az adott mintához ,,legjobb" transzformációt megtalálni! Egy ilyen transzformáció nagy valószínűséggel nem lesz jó a következő mintához. Többet ér, amelyik ugyan gyengébben, de egyenletesen jól teljesít.
Egy sajátos transzformáció az úgynevezett standardizálás vagy studentizálás (standardization, studentization).
Erre akkor van szükség, amikor sokváltozós elemzésben több különböző mértékegységben mért, különböző értéktartományba eső változót kell együtt elemeznünk, és attól tartunk, hogy a nagy értékekkel, illetve az értékek nagy változatosságával bíró változók elnyomják a kis értékű vagy kis variabilitású társaikat.
Azt pedig nem szeretnénk, hogy egy változó mértékegységétől függjön az, hogy milyen szerepet játszhat egy elemzésben.
Ezért minden változót igyekszünk nulla körüli és nagyjából azonos variabilitást mutató változóvá transzformálni.
Ezt úgy érjük el, a változó minden egyes értékéből levonjuk a változó átlagát, majd az így kapott értéket elosztjuk a változó szórásával (a mutatókat lásd ??. fejezetben).
Az eljárást szigorú értelemben akkor nevezhetjük standardizálásnak, ha az elméleti (= populáció-) átlagot vonjuk le és az elméleti (= populációs) szórással osztunk, és akkor studentizálásnak, ha ezeket is a mintából becsüljük.
(A továbbiakban, ha nem okoz félreértést, standardizálásnak nevezzük a studentizálást is.)
Az így átalakított változók átlaga 0, szórása pedig 1 lesz.
Az R-ben a scale() függvénnyel lehet átskálázni adatokat (átskálázás alatt lineáris transzformációt értünk).
Alapértelmezése a studentizálás, az eredmény egy táblázat, amelynek első oszlopa tartalmazza a studentizált adatokat. (Egy egész táblázatot is át lehet egyszerre transzformálni!)
Ötelemű mintára kiszámoljuk a mintaátlagot és a szórást, majd a studentizált értékeket:
(minta<-c(1,4,2,3,6))## [1] 1 4 2 3 6mean(minta)## [1] 3.2sd(minta)## [1] 1.924(stminta <- scale(minta)[,1])## [1] -1.1437 0.4159 -0.6239 -0.1040 1.4557mean(stminta) ## [1] -1.054e-16sd(stminta)## [1] 1Hasonló a célja annak a – szintén különleges – transzformációnak is, amikor a mért értékeket a rangszámaikkal (ranks), azaz az \(1, 2, \ldots , n\) értékekkel helyettesítjük.
A legkisebb érték kapja az 1-est, a második legkisebb a 2-est és így tovább.
Sok statisztikai eljárás dolgozik rangokkal, mint például a Wilcoxon-féle rangösszeg-próba, a Spearman-féle rangkorreláció stb. (lásd 7.6. és 8.2. fejezeteket).
A rang-transzformációval egyenletes eloszlásúvá transzformáljuk az adatokat, amelyeknek így eredeti értéktartományuktól, mértékegységüktől és eloszlásuktól függetlenül ugyanaz lesz az értékkészlete: az 1-től \(n\)-ig terjedő egész számok.
Pontosabban ez csak akkor igaz, ha az értékek között nincsenek egyenlők.
Ha ugyanis az értékek között vannak egyenlők, akkor azok egy igazságos rangsorban ugyanazt a rangszámot kell, hogy kapják.
Igen ám, de mennyi legyen ez az ugyanannyi?
A szokásos megoldás erre az, hogy holtversenyben álló értékek mindegyike a rájuk eső rangok átlagát kapja.
Például, ha a 3-4-5-6 helyen van négyes holtverseny, akkor mind a négy érték a 3, 4, 5, 6 rangok átlagát, 4.5-et kapja.
Így viszont a rangok értékkészlete megváltozik: jelen esetben az 1, 2, 3, 4, 5, 6, 7, 8,… helyett 1, 2, 4.5, 4.5, 4.5, 4.5, 7, 8,… lesz.
Ezért az egyenlő értékek – és az ezekhez tartozó úgynevezett kapcsolt rangok (*ties, tied ranks} – a rangszámokon alapuló statisztikai módszerek alkalmazásánál néha komoly gondokat okoznak.
Egy adatsor értékeiből rangszámokat a rank() függvénnyel készíthetünk.
Figyeljük meg az egyenlő értékekhez tartozó kapcsolt rangokat!
ertekek<-c(21.0, 21.4, 21.4, 23.1, 23.5, 25.0, 25.0, 25.0, 27.2, 28)
(rangok<-rank(ertekek))## [1] 1.0 2.5 2.5 4.0 5.0 7.0 7.0 7.0 9.0 10.0Nyilvánvaló, hogy amikor egy változót egy kevésbé információgazdag skálára transzformálunk, például amikor az életkor változóból előállítjuk a korcsoport változót így: 1 = fiatal (35 év alatti), 2 = középkorú (30–60), 3 = idős (60 év feletti), akkor információt veszítünk. Ezért sokan azt gondolják, hogy egy statisztikai elemzésben az így transzformált változót használva feltétlenül rosszabb, pontatlanabb eredményeket kapunk. Ez azonban tévedés! Ha a pontos életkor nem releváns a vizsgált összefüggés szempontjából, akkor még az is előfordulhat, hogy a korcsoport változóval pontosabb eredményt kapunk, mint az életkorral. Az általános szabály az, hogy releváns információ elhagyása pontatlanabbá, irreleváns információ elhagyása pedig pontosabbá teszi a statisztikai elemzések eredményét.
2.4.4 Hiányzó értékek
Bármennyire gondosan is végezzük a vizsgálatainkat, elkerülhetetlenek az olyan esetek, amikor egy-egy mérés meghiúsul akár egy kísérleti állat elhullása, akár egy minta tönkremenetele vagy szennyeződése miatt.
Az adatrögzítéskor a szóban forgó helyre nem írunk semmit, ezért az adatmátrixból egy vagy több adat hiányozhat, ezek az úgynevezett hiányzó értékek (missing values, missing data).
A számítógépes programok elvileg különbséget tudnak tenni a nulla, a szóköz és a ,,semmit nem írtunk oda" között, de ebben sajnos nem mindig következetesek.
Az Excel például, ha átlagot számol, akkor a szóközt és az üres cellát kihagyja, összeadásnál és szorzásnál viszont nullának veszi őket.
A statisztikai programok legtöbbje a hiányzó értékeket helyesen kezeli: minden számításból kihagyja őket, és bármely velük végzett művelet eredménye ugyancsak hiányzó érték lesz.
Az R a hiányzó értékeket az NA szimbólummal jelöli (olvasd: en-á, az angol ,,not available" rövidítéséből, de megjegyezhetjük úgy is, hogy ,,nincs adat").
Adatfájl előkészítésekor vagy adatok bevitelekor mi is használhatjuk a hiányzó adatok NA-val való jelölését, az R megérti.
Egyes R-függvények rendelkeznek olyan argumentummal, amelynek segítségével beállíthatjuk, hogy mi történjék, ha a függvény NA értékkel találkozik.
Például az átlagot számoló mean() függvénynek az na.rm argumentuma szabályozza ezt. A név az ,,na.remove" rövidítése, ami magyarul ,,az NA-k számításból való eltávolítása", így ha na.rm = TRUE, akkor az NA-k a számításból kimaradnak, ha na.rm = FALSE (ez az alapértelmezés), akkor részt vesznek benne (true = igaz, false = hamis).
Utóbbi esetben, ha az adatok között vannak NA-k, akkor az átlag is NA lesz.
Ezt illusztrálja az alábbi példa, ahol a hianyos.adatok vektor két NA értéket tartalmaz.
hianyos.adatok <- c(122, 27, 194, 5, 182, NA, 126, 81, 106, 197, 75, 114, NA, 127, 118, 175, 195, 83, 88, 38, 177, 138)
mean(hianyos.adatok)## [1] NAmean(hianyos.adatok, na.rm=TRUE)## [1] 118.4Sajnos nem minden függvénynek van ilyen argumentuma, és akkor magunknak kell gondoskodnunk arról, hogy az NA értékek ne okozzanak gondot a számításaink során.
Ehhez használhatjuk az na.omit() függvényt. Az na.omit() az objektumot adja vissza a hiányos sorok nélkül. Egy példa az alkalmazására:
adatok.na.omit <- na.omit(hianyos.adatok)
mean(adatok.na.omit)## [1] 118.4A függvény a hianyos.adatok-ból létrehozott egy olyan objektumot, amelyben az NA-k már nem szerepelnek.
Erre az ,,előkezelt" objektumra már nyugodtan alkalmazhatunk olyan függvényeket is, amelyek nem boldogulnának a hiányzó adatokkal.
Így már az átlagszámításhoz sem kell beállítanunk a na.rm = TRUE-t.
A további függvényekkel kapcsolatban érdemes megnézni az R súgóját.
A hiányzó értékek kezeléséhez hasznos még az is.na() függvény, amellyel azonosíthatjuk a vektorunkban lévő NA-k helyét: a függvény eredményként egy logikai értékekből álló vektort ad vissza, amelynek értéke TRUE vagy FALSE aszerint, hogy az adott helyen NA áll-e vagy sem.
Ennek használatát mutatja be az alábbi R kód:
(hianyzike <- is.na(hianyos.adatok))## [1] FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE(hianyzoksorszamai <- which(hianyzike))## [1] 6 13(hianyzoknelkul <- hianyos.adatok[-hianyzoksorszamai])## [1] 122 27 194 5 182 126 81 106 197 75 114 127 118 175 195 83 88 38 177
## [20] 138A which() függvénnyel meghatároztuk az NA-k sorszámait, majd létrehoztunk egy olyan vektort (hianyzoknelkul), amelyben az NA-k már nem szerepelnek (a szögletes zárójelen belül a mínusz jel azt jelenti, hogy az olyan sorszámúak maradjanak ki a vektorból).
Több statisztikai módszer – például regressziószámítás, faktorelemzés stb. – úgy működik, hogy ha az adatmátrix valamelyik sorában van hiányzó adat, akkor az egész sort kihagyja, vagyis az az eset, amelyiknek akár csak egy adata is hiányzik, teljesen kimarad az elemzésből.
Ezért viszonylag kevés hiányzó érték is – ha elszórtan, különböző sorokban helyezkedik el – erősen lecsökkentheti a feldolgozható mintanagyságot.
Egyetlen hiányzó szám miatt egy egész sort kidobni pazarlásnak tűnik, az ember úgy érzi, hogy a szükségesnél több információt dobunk ki az ablakon.
A hiányzó értékek általában úgy nem pótolhatók, hogy a mérést újra elvégezzük, mert a kísérleti körülmények, a műszerek kalibrálása, az állatok, és még sok minden megváltozhatott időközben.
Ezért dolgoztak ki statisztikai módszereket a hiányzó adatok pótlására: ezt adatpótlásnak vagy imputálásnak (imputting) nevezzük.
(Figyelem, m-mel! Ne keverjük össze az input = adatbevitellel!)
Ezek a módszerek a hiányzó értékeket az adatmátrixban szereplő többi értékből statisztikai becslések segítségével pótolják.
Természetesen az imputálással nyert értékek – mivel a módszerek a többi adatot használják fel a hiányzó értékek pótlására – nem hordoznak új információt, hasznuk csupán annyi, hogy nem kell olyan sok meglévő adatot kidobni a hiányzó értékek miatt.
A hiányzó értékek pótlása, illetve az egyes statisztikai módszerek átalakítása úgy, hogy hiányzó értékek mellett is működőképesek maradjanak, egy ,,külön tudomány" vagy inkább művészet, amely jócskán meghaladja e könyv kereteit.
Olyannyira, hogy több, csupán e témával foglalkozó monográfia is megjelent, amelyek közül az egyik leghíresebb: (Little and Rubin (2014)).
Ha a hiányzó értékek száma eléri vagy meghaladja a releváns adatok 10%-át, akkor már jobb, ha az adatokat félretesszük, és inkább azon gondolkodunk, hogyan tudnánk egy megbízhatóbb kísérleti protokollt kidolgozni, amely biztosítja, hogy kevesebb hiányzó adat keletkezzék. Ilyen sok hiányzó érték esetén ugyanis senki nem fogja elhinni az eredményeinket. Szimulált adatokkal – vagy akár saját valódi adataival – a Kedves Olvasó is kipróbálhatja, hogy a legtöbb adathalmazból levonható következtetés megváltoztatható, sőt ellenkezőjére fordítható az adatok 10–15%-ának ,,ügyes" elhagyásával.
2.4.5 Kiugró értékek
Az is gyakran előfordul, hogy egyes adatok ,,kilógnak a sorból". Lehet, hogy egy érték egyenesen képtelenség, de lehet, hogy csak gyanúsan eltér a többitől. Az ilyen értékeket kiugró értékeknek (outlier) nevezzük. Tipikus, hogy ezeket már csak az adatok elemzése során vesszük észre, sőt, valószínűleg csak az elemzés későbbi fázisaiban. Például a 2.6. ábrán látható – nyíllal jelölt – kiugró érték csak a két változó együttes elemzésekor tűnik fel, ha csak az \(x\)-et vagy csak az \(y\)-t nézzük, akkor nem.
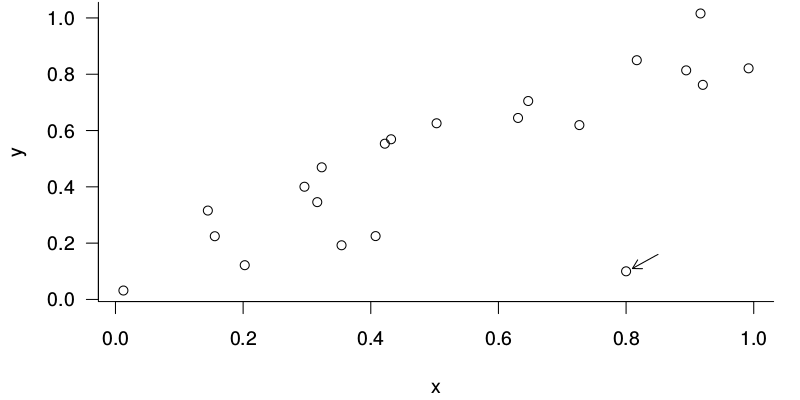
2.6: ábra. Kiugró érték
Mivel egy kiugró érték oka lehet elírás vagy adatrögzítési hiba is, általános szabály, hogy ilyenkor a hibásnak tűnő adatot ellenőrizni kell a keletkezésétől kezdve egészen az adatmátrixba kerüléséig. Ugyancsak ellenőrizni kell a kísérleti jegyzőkönyvet, hátha abban feljegyeztek valamely olyan körülményt, amely magyarázza az adat furcsaságát. Többek között ezért is meg kell őriznünk az eredeti mérési bizonylatokat, kísérleti jegyzőkönyveket.
Ha semmi olyan körülményt nem találunk, amelynek alapján az érték javítható volna, akkor vagy úgy gondoljuk, hogy furcsa ugyan, de úgy látszik, ilyen érték is előfordulhat, vagy továbbra is azt gondoljuk, hogy ez lehetetlen, valami hiba van a dologban. Érdemes ilyenkor irodalomkutatást is végezni, találtak-e már mások is hasonlót. Ha végül úgy döntünk, hogy az érték képtelenség, akkor elhagyhatjuk. Kétséges esetben ajánlatos elvégezni az elemzést így is, úgy is, hogy pontosan lássuk, mi lesz a különbség az eredmények között. Az outlierekre még fokozottabban érvényes, amit a hiányzó értékekkel kapcsolatban mondtunk: ha túl sok értéket kiugró értéknek tekintünk és elhagyunk, akkor ezzel az eredményeket jelentős mértékben befolyásolhatjuk. Ha az eredményekből közlemény születik, abban mindenképpen meg kell említeni, hogy voltak-e kiugró értékek, amelyeket elhagytunk – már csak azért is, mert ha a vizsgált jelenség olyan, hogy időről időre előfordulnak benne szélsőséges eredmények, de senki sem közli őket, akkor lehet, hogy sohasem fog kiderülni a létezésük. Gondoljunk arra, lehet, hogy épp a kiugró értékek a legfontosabb megfigyeléseink, amikből valami újat fogunk tanulni!
Elkerülendő a szubjektivitást, több módszert is kitaláltak annak eldöntésére, hogy mi számítson kiugró értéknek, és mi nem.
Az R is ez utóbbiakat tekinti kiugró értéknek.
Ezeket a boxplot.stats() függvénnyel számolás nélkül megtalálhatjuk, mint azt a következő példa mutatja.
2.6. példa: Elsőéves hallgatók testmagassága – kiugró értékek
Az elsőéves egyetemisták testmagasság adatai közül kikeressük azokat az értékeket, amelyek a fenti kritérium szerint kiugró értéknek számítanak.
Ezeket a boxplot.stats() függvény out néven adja vissza:
boxplot.stats(pop$magas)$out## [1] 158 197 161 197 160 160 195Természetesen az ilyen módszerek csak arra valók, hogy olyan ,,gyanús" értékeket találhassunk, amelyeket esetleg érdemes ellenőriznünk, de a talált értékekről nem bizonyítják, hogy valóban gond lenne velük. Sőt, az ilyen kritériumok mechanikus alkalmazásakor az embert az a kellemetlen meglepetés érheti, hogy talál egy kiugró értéket, elhagyja, majd ellenőrizvén a maradék adatokat ugyanazzal a kritériummal – mivel az első elhagyása megváltoztatta a mintát – megint talál egyet, és így tovább. Rossz esetben elfogyhat a minta. Ilyenkor (már akkor is, ha az első outlier elhagyása után megjelenik még egy!) mindig jusson eszünkbe, hogy talán nem is kiugró értékekkel van dolgunk, hanem egy egyik irányba elnyúló, ferde eloszlással (vagyis hogy talán már az első sem volt az!), és próbálkozzunk inkább valami olyan elemzéssel, amely ferde eloszlásokkal is jól működik!
Általában is fontos eldöntendő kérdés, hogy a többitől távol eső, nem tipikus megfigyeléseket szemétnek tekintjük-e, vagy a vizsgált folyamat szerves részének, amelyek elhagyása meghamisítaná az eredményeket. A parazitológiában például ismert, hogy a paraziták gazdákon való eloszlása jellemzően aggregált, azaz a legtöbb gazdán csak kevés parazita található, a paraziták többsége néhány igen fertőzött gazdán koncentrálódik. Ha ezeket, mint nem tipikusakat elhagynánk, akkor ezzel a jelenség lényegi részétől – egyben a parazita-populáció döntő többségétől – válnánk meg.
Ha úgy látjuk, hogy a kiugró értékek valójában nem tartoznak a vizsgált folyamathoz, akkor úgynevezett robusztus módszereket kell alkalmaznunk, amelyek az outliereket képesek figyelmen kívül hagyni. A robusztus módszerekről lásd Jureckova, Picek, and Schindler (2019) könyvét. Tehát, ha robusztus módszert alkalmazunk, akkor a kiugró értékeket nem kell saját kezűleg elhagynunk, a módszer maga gondoskodik róla, hogy ne sok vizet zavarhassanak. Viszont nagy hiba a robusztus módszerek alkalmazása akkor, ha a távoleső értékek a folyamat szerves részét alkotják. Ilyenkor az egyik lehetőség, hogy nemparaméteres vagy eloszlásfüggetlen módszerrel próbálkozunk, a másik pedig, hogy olyan paraméteres módszerrel, amelyet éppen a szóban forgóhoz hasonló ferde eloszlásokra dolgoztak ki. Ezek a módszerek ugyanis a távol eső értékeket is megfelelően figyelembe tudják venni a számításokban. Ha viszont a távol eső értékek nem tartoznak a folyamathoz, akkor épp e módszerek alkalmazása ad félrevezető eredményt.
2.5 Összefogalók
2.1 Populáció és minta
- Megfigyelési vagy mintavételi egység: a vizsgálat alanya vagy tárgya, amelyen a méréseket, vizsgálatokat végezzük.
- Minta: a ténylegesen megvizsgált, illetve vizsgálatra kiválasztott megfigyelési egységek halmaza.
- Populáció vagy alapsokaság: az összes lehetséges, szóba jöhető mintavételi egységet tartalmazó halmaz, amelynek a minta részhalmaza. Mindig a populáció az a kör, amelyre a vizsgálat irányul.
2.2 Leíró és induktív statisztika
- Leíró statisztika:
- az adatokban rejlő információ emészthető formában való tálalásával foglalkozik
- adatok rendezése, csoportosítása (táblázatok), megjelenítése (grafikonok), statisztikai mérőszámokkal való jellemzése (minimum, maximum, átlag, szórás stb.)
- Induktív statisztika
- egy minta vizsgálatából vonunk le a populációra érvényes következtetéseket
- becslések és hipotézisvizsgálatok
2.3 Mintavételi módszerek
- Az induktív statisztikában a mintából vonunk le a populációra érvényes következtetéseket.
- A mintavétel módjától függnek, hogy az elemzésre milyen eljárások használhatók.
Egyszerű véletlen mintavétel
- Az alapsokaság minden egyede egyforma eséllyel kerül a mintába.
- A mintavétel
- visszatevéses vagy
- visszatevés nélküli.
- Végtelen populáció vagy visszatevéses mintavétel esetén a mintabeli értékek mint valószínűségi változók függetlenek egymástól
- Ez a legtöbb klasszikus statisztikai eljárás alkalmazhatóságának egyik feltétele.
Reprezentativitás
- Ha a mintavételt a véletlenre bízzuk, akkor lehet, hogy a minta nem lesz reprezentatív.
- Ha valamilyen szempontból fontos a reprezentativitás, akkor aszerint a szempont szerint érdemes rétegeznünk.
- Véletlen mintavétel esetén bármely a mintából számított érték (minimum, maximum, átlag stb.) – a minta véletlenségéből következően – egy olyan véletlen szám (valószínűségi változó) lesz, amelynek eloszlása a valószínűségszámítás segítségével kiszámítható.
2.4.1 Adatmátrix
Az adatmátrix minden sora egy megfigyelési egység: eset, oszlopai pedig az egyes mért vagy megfigyelt adatoknak felelnek meg: változó.
2.4.2 Adattípusok, mérési skálák
- Kvalitatív változók (faktorok)
- nominális
- csak megnevez, kategorizál, csoportba sorol, kódol
- ordinális
- csoportba sorol, de értékeinek egyértelmű természetes sorrendje van
- nominális
- Kvantitatív változók (numerikus)
- diszkrét
- összes lehetséges értékét fel tudjuk sorolni
- diszkrét
- folytonos
- lehetséges értékei a számegyenesen egy folytonos tartományt alkotnak
2.4.3 Transzformációk, származtatott változók
Származtatott változó
- Olyan változó, amelyet nem megfigyelünk, hanem más változókból matematikai vagy logikai műveletekkel számolunk ki.
Eloszlás típusok
- Egy tartományon egyenletes eloszlásról akkor beszélünk, ha a tartomány egyik részében sem sűrűbb a pontok mintázata, mint másutt.
- Egycsúcsú eloszlásról akkor beszélünk, ha a megfigyelések a tartományban egy hely környékén sűrűbbek, mint másutt,
- többcsúcsúról akkor, ha több ilyen sűrűsödési hely van.
- Ferde eloszlás az olyan, amelyik egycsúcsú ugyan, de nem szimmetrikus: a sűrűsödési helytől balra és jobbra távolodva a pontok sűrűsége nem azonos mértékben csökken.
- A nagyobb értékek irányában (jobbra, felfelé, + irányban) elnyúló eloszlást jobbra ferdének nevezzük.
- A kisebb értékek felé (balra, lefelé, - irányban) elnyúlót pedig balra ferdének nevezzük.
Normális eloszlás
- A normális vagy Gauss-eloszlás egycsúcsú, szimmetrikus eloszlás: a sűrűsödési hely a tartomány közepén van, és tőle balra és jobbra a pontok sűrűsége a távolságtól függően ugyanolyan ütemben csökken.
Gyakori transzformációk azért, hogy az eloszlás normális legyen
- Jobbra ferde eloszlás esetén: gyök- vagy a logaritmus-transzformáció;
- Balra ferde eloszlás esetén: hatvány- vagy exponenciális függvénnyel való transzformáció.
- Ezek mind úgy működnek, hogy megváltoztatják az értékek közötti távolságokat: az értéktartomány egyik szélén nyújtják, a másikon pedig összenyomják a skálát.
- Relatív gyakoriságokra például az arcsin (arkusz szinusz) függvényt szokták ajánlani
- A sikerre nincs garancia, előfordulhat, hogy az eloszlást semmilyen transzformációval nem tudjuk – még közelítőleg sem – normálissá tenni.
- Megtörténhet, hogy az eredeti adatok biológiailag jól interpretálhatók, a transzformált adatoknak viszont már nem tudunk biológiai jelentést tulajdonítani, ilyenkor inkább ne transzformáljunk, hanem keressünk ferde eloszlásokkal is működő módszereket!
Standardizálás és studentizálás
- Ha több különböző mértékegységben mért, különböző értéktartományba eső változót kell együtt elemeznünk, minden változót igyekszünk nulla körüli és nagyjából azonos variabilitást mutató változóvá transzformálni.
- A változó minden egyes értékéből levonjuk a változó átlagát, majd az így kapott értéket elosztjuk a változó szórásával. Az így átalakított változók átlaga 0, szórása pedig 1 lesz.
Rangtranszformáció
- A mért értékeket a rangszámaikkal, azaz az \(1, 2, ... , n\) értékekkel helyettesítjük.
- A rang-transzformációval egyenletes eloszlásúvá transzformáljuk az adatokat, amelyeknek így eredeti értéktartományuktól, mértékegységüktől és eloszlásuktól függetlenül ugyanaz lesz az értékkészlete: az 1-től n-ig terjedő egész számok.
- Ha az értékek között vannak egyenlők, akkor a holtversenyben álló értékek mindegyike a rájuk eső rangok átlagát kapja (kapcsolt rangok).
Megjegyzések
- Nyilvánvaló, hogy amikor egy változót egy kevésbé információ gazdag skálára transzformálunk, akkor információt veszítünk.
- Ez azonban nem jelenti azt, hogy feltétlenül rosszabb, pontatlanabb eredményeket kapunk.
- Az általános szabály az, hogy releváns információ elhagyása pontatlanabbá, irreleváns információ elhagyása pedig pontosabbá teszi a statisztikai elemzések eredményét.
2.4.4 Hiányzó értékek
- Az adatmártixból különböző okokból hiányozhatnak adatok.
- A hiányzó értékek általában úgy nem pótolhatók, hogy a mérést újra elvégezzük, mert a kísérleti körülmények, a műszerek kalibrálása, az állatok, és még sok minden megváltozhatott időközben.
- Ha az adatok között vannak
NA-k, akkor az átlag isNAlesz. - Egyes R-függvények rendelkeznek olyan argumentummal, amelynek segítségével beállíthatjuk, hogy mi történjék, ha a függvény értékkel találkozik.
- Nem minden függvénynek van ilyen argumentuma, ekkor külön el kell távolítani az
NA-kat tartalmazó sorokat a táblázatból. - Több statisztikai módszer úgy működik, hogy ha az adatmátrix valamelyik sorában van hiányzó adat, akkor az egész sort kihagyja. Ezért viszonylag kevés hiányzó érték is erősen lecsökkentheti a feldolgozható mintanagyságot.
- Statisztikai módszerek a hiányzó adatok pótlására: adatpótlásnak vagy imputálásnak nevezzük
- A hiányzó értékeket az adatmátrixban szereplő többi értékből statisztikai becslések segítségével pótolják.
- Az imputálással nyert értékek nem hordoznak új információt.
- Ha a hiányzó értékek száma eléri vagy meghaladja a releváns adatok 10%-át, akkor már jobb, ha az adatokat nem is elemezzük.
2.4.5 Kiugró értékek
- Gyakran előfordul, hogy egyes adatok ,,kilógnak a sorból".
- Az ilyen értékeket kiugró értékeknek outlier nevezzük.
- A hibásnak tűnő adatot ellenőrizni kell.
- Ha úgy döntünk, hogy az érték képtelenség, akkor elhagyhatjuk.
- Kétséges esetben ajánlatos elvégezni az elemzést így is, úgy is, hogy pontosan lássuk, mi lesz a különbség az eredmények között.
- Ha túl sok értéket kiugró értéknek tekintünk és elhagyunk, akkor ezzel az eredményeket jelentős mértékben befolyásolhatjuk.
- Több módszert is kitaláltak annak eldöntésére, hogy mi számítson kiugró értéknek, és mi nem.
- Ha úgy látjuk, hogy a kiugró értékek valójában nem tartoznak a vizsgált folyamathoz, akkor úgynevezett robusztus módszereket kell alkalmaznunk, amelyek az outliereket képesek figyelmen kívül hagyni.